【题目】函数g(x)=f(x)+2x,x∈R为奇函数.
(1)判断函数f(x)的奇偶性;
(2)若x>0时,f(x)=log3x,求函数g(x)的解析式.
参考答案:
【答案】
(1)解:任给x∈R,f(x)=g(x)﹣2xf(﹣x)=g(﹣x)+2x…(2分)
因为g(x)为奇函数,所以g(﹣x)=﹣g(x),
所以f(﹣x)=﹣g(x)+2x=﹣f(x),
所以f(x)为奇函数
(2)解:当x>0时,g(x)=log3x+2x
当x<0时,﹣x>0,所以g(﹣x)=log3(﹣x)﹣2x
因为 g(x)为奇函数
所以 g(x)=﹣g(﹣x)=﹣[log3(﹣x)﹣2x]=2x﹣log3(﹣x)
又因为奇函数g(0)=0
所以g(x)= 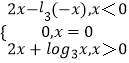
【解析】(1)函数g(x)=f(x)+2x(x∈R)为奇函数,g(﹣x)=f(﹣x)﹣2x=﹣g(x)=﹣f(x)﹣2x,可得f(﹣x)=﹣f(x),即可判断函数f(x)的奇偶性;(2)若x>0时,f(x)=log3x,求出x<0,x=0时的解析式,即可求函数g(x)的解析式.
【考点精析】认真审题,首先需要了解奇偶性与单调性的综合(奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性).
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a是实数,f(x)=a﹣
 (x∈R).
(x∈R).
(1)证明不论a为何实数,f(x)均为增函数;
(2)若f(x)满足f(﹣x)+f(x)=0,解关于x的不等式f(x+1)+f(1﹣2x)>0. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)若
 ,求函数
,求函数 的极值;
的极值;(Ⅱ)若
 ,
,  ,
,  ,使得
,使得 (
( ),求实数
),求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知幂函数f(x)=(﹣2m2+m+2)xm+1为偶函数.
(1)求f(x)的解析式;
(2)若函数y=f(x)﹣2(a﹣1)x+1在区间(2,3)上为单调函数,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(
 )x , 函数g(x)=log
)x , 函数g(x)=log 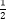 x.
x.
(1)若g(ax2+2x+1)的定义域为R,求实数a的取值范围;
(2)当x∈[( )t+1 , (
)t+1 , (  )t]时,求函数y=[g(x)]2﹣2g(x)+2的最小值h(t);
)t]时,求函数y=[g(x)]2﹣2g(x)+2的最小值h(t);
(3)是否存在非负实数m,n,使得函数y=log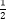 f(x2)的定义域为[m,n],值域为[2m,2n],若存在,求出m,n的值;若不存在,则说明理由.
f(x2)的定义域为[m,n],值域为[2m,2n],若存在,求出m,n的值;若不存在,则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
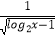 的定义域是 ( )
的定义域是 ( )
A.{x|x≥2}
B.{x|x≤2}
C.{x|x>2}
D.{x|x<2} -
科目: 来源: 题型:
查看答案和解析>>【题目】过点
 的直线
的直线 与中心在原点,焦点在
与中心在原点,焦点在 轴上且离心率为
轴上且离心率为 的椭圆
的椭圆 相交于
相交于 、
、 两点,直线
两点,直线 过线段
过线段 的中点,同时椭圆
的中点,同时椭圆 上存在一点与右焦点关于直线
上存在一点与右焦点关于直线 对称.
对称.(1)求直线
 的方程;
的方程;(2)求椭圆
 的方程.
的方程.
相关试题

