搜索
【题目】过点
的直线
与中心在原点，焦点在
轴上且离心率为
的椭圆
相交于
、
两点，直线
过线段
的中点，同时椭圆
上存在一点与右焦点关于直线
对称．
（1）求直线
的方程；
（2）求椭圆
的方程．
参考答案：
【答案】(1) 
;(2) 
.
【解析】试题分析： 
根据离心率大小可以得到
的值，设出椭圆的方程；因为
在椭圆上，代入椭圆方程，得到两个等式，根据这两个等式表示出直线
的斜率。直线
过线段
的中点
，故该中点满足
，由此可以求出
的关系，代入直线
斜率的表达式中即可求得
，又直线过点
，故可求出直线
的方程；
椭圆
上存在一点与右焦点
关于直线
对称，列出方程组，求出
的值，从而得到椭圆的方程。
解析：（1）由
，得
，从而
设椭圆方程为
在椭圆上，则
两式相减得，
设
的中点为
则
又
在直线
上， 
，于是
，则直线
的方程为
.
（2）右焦点
关于直线
的对称点设为
则
解得
由点
在椭圆上，得
，
所求椭圆
的方程的方程为
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】函数g（x）=f（x）+2x，x∈R为奇函数．
（1）判断函数f（x）的奇偶性；
（2）若x＞0时，f（x）=log3x，求函数g（x）的解析式． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=（
）x ， 函数g（x）=log 
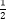x．
（1）若g（ax2+2x+1）的定义域为R，求实数a的取值范围；
（2）当x∈[（ ）t+1 ， （ ）t]时，求函数y=[g（x）]2﹣2g（x）+2的最小值h（t）；
（3）是否存在非负实数m，n，使得函数y=log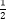 f（x2）的定义域为[m，n]，值域为[2m，2n]，若存在，求出m，n的值；若不存在，则说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】函数f（x）=
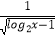的定义域是 （ ）
A.{x|x≥2}
B.{x|x≤2}
C.{x|x＞2}
D.{x|x＜2} -
科目： 来源： 题型：
查看答案和解析>>【题目】选修4-4：坐标系与参数方程
在极坐标系中，点
的极坐标是
，曲线 
的极坐标方程为
.以极点为坐标原点，极轴为 
轴的正半轴建立平面直角坐标系，斜率为 
的直线 
经过点
.（1）写出直线
的参数方程和曲线 
的直角坐标方程；（2）若直线
和曲线
相交于两点
，求
的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】下列函数在（0，+∞）上单调递增的是（ ）
A.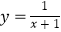
B.y=（x﹣1）2
C.y=21﹣x
D.y=lg（x+3） -
科目： 来源： 题型：
查看答案和解析>>【题目】某农科所发现，一种作物的年收获量
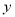（单位：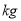 
）与它“相近”作物的株数 
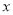具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 
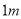)，并分别记录了相近作物的株数为 
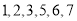时，该作物的年收获量的相关数据如下：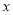 
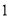
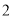
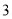
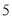
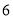
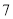
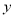
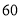
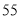
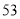
（1）求该作物的年收获量
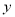关于它“相近”作物的株数
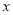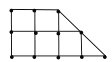
的线性回归方程；（2）农科所在如图所示的直角梯形地块的每个格点（指纵、横直线的交叉点）处都种了一株该作物，图中
每个小正方形的边长均为
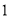，若从直角梯形地块的边界和内部各随机选取一株该作物，求这两株作物 “相近”且年产量仅相差
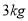的概率．附：对于一组数据
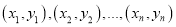，其回归直线
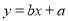的斜率和截距的最小二乘估计分别为,
, 
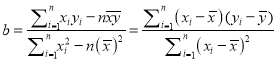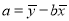
相关试题
