【题目】函数f(x)= ![]() 的定义域是 ( )
的定义域是 ( )
A.{x|x≥2}
B.{x|x≤2}
C.{x|x>2}
D.{x|x<2}
参考答案:
【答案】C
【解析】解:∵函数f(x)= ![]() ,
,
∴ ![]() ≠0,
≠0,
即log2x﹣1>0,
∴log2x>1;
解得x>2,
∴f(x)的定义域是{x|x>2}.
故选:C.
【考点精析】解答此题的关键在于理解函数的定义域及其求法的相关知识,掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知幂函数f(x)=(﹣2m2+m+2)xm+1为偶函数.
(1)求f(x)的解析式;
(2)若函数y=f(x)﹣2(a﹣1)x+1在区间(2,3)上为单调函数,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数g(x)=f(x)+2x,x∈R为奇函数.
(1)判断函数f(x)的奇偶性;
(2)若x>0时,f(x)=log3x,求函数g(x)的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(
 )x , 函数g(x)=log
)x , 函数g(x)=log 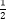 x.
x.
(1)若g(ax2+2x+1)的定义域为R,求实数a的取值范围;
(2)当x∈[( )t+1 , (
)t+1 , (  )t]时,求函数y=[g(x)]2﹣2g(x)+2的最小值h(t);
)t]时,求函数y=[g(x)]2﹣2g(x)+2的最小值h(t);
(3)是否存在非负实数m,n,使得函数y=log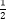 f(x2)的定义域为[m,n],值域为[2m,2n],若存在,求出m,n的值;若不存在,则说明理由.
f(x2)的定义域为[m,n],值域为[2m,2n],若存在,求出m,n的值;若不存在,则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】过点
 的直线
的直线 与中心在原点,焦点在
与中心在原点,焦点在 轴上且离心率为
轴上且离心率为 的椭圆
的椭圆 相交于
相交于 、
、 两点,直线
两点,直线 过线段
过线段 的中点,同时椭圆
的中点,同时椭圆 上存在一点与右焦点关于直线
上存在一点与右焦点关于直线 对称.
对称.(1)求直线
 的方程;
的方程;(2)求椭圆
 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,点
 的极坐标是
的极坐标是 ,曲线
,曲线  的极坐标方程为
的极坐标方程为 .以极点为坐标原点,极轴为
.以极点为坐标原点,极轴为  轴的正半轴建立平面直角坐标系,斜率为
轴的正半轴建立平面直角坐标系,斜率为  的直线
的直线  经过点
经过点 .
.(1)写出直线
 的参数方程和曲线
的参数方程和曲线  的直角坐标方程;
的直角坐标方程;(2)若直线
 和曲线
和曲线 相交于两点
相交于两点 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数在(0,+∞)上单调递增的是( )
A.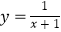
B.y=(x﹣1)2
C.y=21﹣x
D.y=lg(x+3)
相关试题

