【题目】已知向量 ![]() 与
与 ![]() .
.
(Ⅰ)若 ![]() 在
在 ![]() 方向上的投影为
方向上的投影为 ![]() ,求λ的值;
,求λ的值;
(Ⅱ)命题P:向量 ![]() 与
与 ![]() 的夹角为锐角;
的夹角为锐角;
命题q: ![]() ,其中向量
,其中向量 ![]() ,
, ![]() =(
=( ![]() )(λ,α∈R).若“p或q”为真命题,“p且q”为假命题,求λ的取值范围.
)(λ,α∈R).若“p或q”为真命题,“p且q”为假命题,求λ的取值范围.
参考答案:
【答案】解:(Ⅰ)由已知, ![]() 在
在 ![]() 方向上的投影
方向上的投影 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() .
.
所以1﹣2λ=5,∴λ=﹣2.
(Ⅱ)1°,若p为真,则 ![]() >0,且
>0,且 ![]() ,即1﹣2λ>0,且λ≠﹣2.
,即1﹣2λ>0,且λ≠﹣2.
2°若p为真,由 ![]() 得λ2﹣cos2α=λ+2sinα,
得λ2﹣cos2α=λ+2sinα,
∴λ2﹣λ=cos2α+2sinα=1﹣sin2α+2sinα=﹣(sinα﹣1)2+2.
∵﹣1≤sinα≤1,∴﹣2≤λ2﹣λ≤2,∴﹣1≤λ≤2.
若p真q假,则  ∴λ<﹣1且λ≠﹣2.
∴λ<﹣1且λ≠﹣2.
若p假q真,则  ∴
∴ ![]() ≤λ≤2
≤λ≤2
综上得λ∈(﹣∞,﹣2)∪(﹣2,﹣1)∪[ ![]() ,2]
,2]
【解析】(Ⅰ) ![]() 在
在 ![]() 方向上的投影的表达式是
方向上的投影的表达式是 ![]() ,由此得出关于λ的方程,解出即可.(Ⅱ)若“p或q”为真命题,“p且q”为假命题,则pq中一真一假,分类求解,再合并即可.
,由此得出关于λ的方程,解出即可.(Ⅱ)若“p或q”为真命题,“p且q”为假命题,则pq中一真一假,分类求解,再合并即可.
【考点精析】解答此题的关键在于理解复合命题的真假的相关知识,掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真,以及对数量积表示两个向量的夹角的理解,了解设![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 的夹角,则
的夹角,则 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
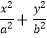 =1(a>b>0)的焦距为2
=1(a>b>0)的焦距为2  ,长轴长为4.
,长轴长为4.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)如图,过坐标原点O作两条互相垂直的射线,与椭圆C交于A,B两点.设A(x1 , y1),B(x2 , y2),直线AB的方程为y=﹣2x+m(m>0),试求m的值.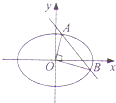
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
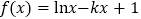 (
(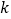 为常数),函数
为常数),函数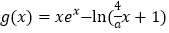 ,(
,(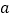 为常数,且
为常数,且 ).
).(1)若函数
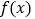 有且只有1个零点,求
有且只有1个零点,求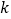 的取值的集合.
的取值的集合.(2)当(1)中的
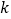 取最大值时,求证:
取最大值时,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列{an}的首项为8,Sn是其前n项的和,某同学经计算得S2=20,S3=36,S4=65,后来该同学发现了其中一个数算错了,则该数为( )
A.S1
B.S2
C.S3
D.S4 -
科目: 来源: 题型:
查看答案和解析>>【题目】以下几个结论中:①在△ABC中,有等式
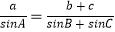 ②在边长为1的正△ABC中一定有
②在边长为1的正△ABC中一定有 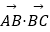 =
= 
③若向量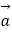 =(﹣3,2),
=(﹣3,2), 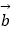 =(0,﹣1),则向量
=(0,﹣1),则向量 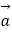 在向量
在向量 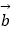 方向上的投影是﹣2
方向上的投影是﹣2
④与向量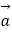 =(﹣3,4)同方向的单位向量是
=(﹣3,4)同方向的单位向量是 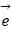 =(﹣
=(﹣  ,
,  )
)
⑤若a=40,b=20,B=25°,则满足条件的△ABC仅有一个;
其中正确结论的序号为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级,某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.

(1)若销售金额(单位:万元)不低于平均值
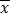 的微商定义为优秀微商,其余为非优秀微商,根据茎叶图推断该地区110家微商中有几家优秀?
的微商定义为优秀微商,其余为非优秀微商,根据茎叶图推断该地区110家微商中有几家优秀?(2)从随机抽取的6家微商中再任取2家举行消费者回访调查活动,求恰有1家是优秀微商的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
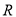 上的函数
上的函数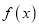 对任意
对任意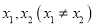 都有
都有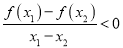 ,且函数
,且函数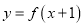 的图象关于原点对称,若
的图象关于原点对称,若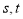 满足不等式
满足不等式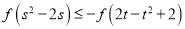 ,则当
,则当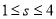 时,
时, 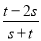 的取值范围是( )
的取值范围是( )A.
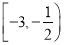 B.
B. 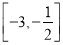 C.
C. 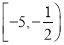 D.
D. 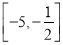
相关试题

