【题目】已知函数![]() (
(![]() 为常数),函数
为常数),函数![]() ,(
,(![]() 为常数,且
为常数,且![]() ).
).
(1)若函数![]() 有且只有1个零点,求
有且只有1个零点,求![]() 的取值的集合.
的取值的集合.
(2)当(1)中的![]() 取最大值时,求证:
取最大值时,求证:![]() .
.
参考答案:
【答案】(1) {k|k≤0或k=1} (2)见解析
【解析】试题分析:
(1)由题意得![]() ,①当k≤0时,由根的存在性定理可得f(x)在(ek-2,1)上存在唯一零点,符合题意。②当k>0时,可得f(x)在
,①当k≤0时,由根的存在性定理可得f(x)在(ek-2,1)上存在唯一零点,符合题意。②当k>0时,可得f(x)在![]() 上单调递增,在
上单调递增,在![]() 上单调递减。若
上单调递减。若![]() ,得k=1,显然满足题意;若
,得k=1,显然满足题意;若![]() ,则得
,则得![]() 在
在![]() 上有唯一零点,在
上有唯一零点,在![]() 上有唯一零点,不符题意。综上可得实数k的取值的集合为{k|k≤0或k=1}.
上有唯一零点,不符题意。综上可得实数k的取值的集合为{k|k≤0或k=1}.
(2)由(1)知k=1,可得lnx≤x-1,而![]() ,故
,故![]() 。故当k=1时,
。故当k=1时,![]()
![]()
![]() 。 再证记
。 再证记![]() ,即可得到结论。
,即可得到结论。
试题解析:
(1)由题意得![]() ,
,
①当k≤0时,f′(x)>0,则f(x)在(0,+∞)单调递增.
而f(ek-2)=k-2-kek-2+1=k(1-ek-2)-1≤-1<0,f(1)=1-k>0,
故f(x)在(ek-2,1)上存在唯一零点,满足题意;
②当k>0时,
令f′(x)>0得0<x<![]() ,则f(x)在
,则f(x)在![]() 上单调递增;
上单调递增;
令f′(x)<0得x>![]() ,则f(x)在
,则f(x)在![]() 上单调递减;
上单调递减;
若![]() ,得k=1,显然满足题意;
,得k=1,显然满足题意;
若![]() ,则0<k<1,而f
,则0<k<1,而f![]() =
=![]() <0,
<0,
又f![]() =2ln
=2ln![]() -
-![]() +1=2
+1=2![]() +1,
+1,
令h(x)=lnx-x+1,则h′(x)=![]() ,
,
令h′(x)>0,得x<1,故h(x)在(0,1)上单调递增;
令h′(x)<0,得x>1,故h(x)在(1,+∞)上单调递减;
故h(x)≤h(1)=0,则h![]() =ln
=ln![]() -
-![]() +1<0,
+1<0,
即ln![]() -
-![]() <-1,
<-1,
则f![]() =2ln
=2ln![]() -
-![]() +1=2
+1=2![]() +1<-1<0.
+1<-1<0.
故![]() 在
在![]() 上有唯一零点,在
上有唯一零点,在![]() 上有唯一零点,不符题意.
上有唯一零点,不符题意.
综上实数k的取值的集合为{k|k≤0或k=1}.
(2)由(1)知k=1,可得lnx≤x-1,当且仅当x=1时等号成立,
而![]() ,故
,故![]() ,
,
则k=1时,![]()
![]() 。
。
记![]() ,
,
则F′(x)=(x+1)![]() =
=![]() (axex-2),
(axex-2),
令G(x)=axex-2,则G′(x)=a(x+1)ex>0,故G(x)在(0,+∞)上单调递增.
而G(0)=-2<0,G![]() =2(
=2(![]() -1)>0,
-1)>0,
故存在x0∈![]() ,使得G(x0)=0,即ax0
,使得G(x0)=0,即ax0![]() -2=0.
-2=0.
且当x∈(0,x0)时,G′(x)<0,故F′(x)<0;
当x∈(x0,+∞)时,G′(x)>0,故F′(x)>0.
则F(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,
故![]()
![]()
故ag(x)-2f(x)>2(lna-ln2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=
 是(﹣∞,+∞)上的减函数,那么a的取值范围是
是(﹣∞,+∞)上的减函数,那么a的取值范围是 -
科目: 来源: 题型:
查看答案和解析>>【题目】求函数y=loga(x﹣x2)(a>0,a≠1)的单调区间及值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
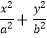 =1(a>b>0)的焦距为2
=1(a>b>0)的焦距为2 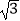 ,长轴长为4.
,长轴长为4.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)如图,过坐标原点O作两条互相垂直的射线,与椭圆C交于A,B两点.设A(x1 , y1),B(x2 , y2),直线AB的方程为y=﹣2x+m(m>0),试求m的值.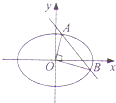
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列{an}的首项为8,Sn是其前n项的和,某同学经计算得S2=20,S3=36,S4=65,后来该同学发现了其中一个数算错了,则该数为( )
A.S1
B.S2
C.S3
D.S4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 与
与  .
.
(Ⅰ)若 在
在  方向上的投影为
方向上的投影为  ,求λ的值;
,求λ的值;
(Ⅱ)命题P:向量 与
与  的夹角为锐角;
的夹角为锐角;
命题q: ,其中向量
,其中向量  ,
,  =(
=(  )(λ,α∈R).若“p或q”为真命题,“p且q”为假命题,求λ的取值范围.
)(λ,α∈R).若“p或q”为真命题,“p且q”为假命题,求λ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】以下几个结论中:①在△ABC中,有等式
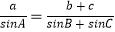 ②在边长为1的正△ABC中一定有
②在边长为1的正△ABC中一定有 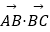 =
= 
③若向量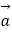 =(﹣3,2),
=(﹣3,2), 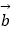 =(0,﹣1),则向量
=(0,﹣1),则向量 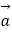 在向量
在向量 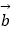 方向上的投影是﹣2
方向上的投影是﹣2
④与向量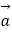 =(﹣3,4)同方向的单位向量是
=(﹣3,4)同方向的单位向量是 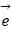 =(﹣
=(﹣  ,
,  )
)
⑤若a=40,b=20,B=25°,则满足条件的△ABC仅有一个;
其中正确结论的序号为 .
相关试题

