【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对![]() 名六年级学生进行了问卷调查,得到如下列联表(平均每天喝
名六年级学生进行了问卷调查,得到如下列联表(平均每天喝![]() 以上为常喝,体重超过
以上为常喝,体重超过![]() 为肥胖):
为肥胖):
常喝 | 不常喝 | 合计 | |
肥胖 |
|
|
|
不胖 |
|
|
|
合计 |
|
|
|
(1)已知在全部![]() 人中随机抽取
人中随机抽取![]() 人,求抽到肥胖的学生的概率?
人,求抽到肥胖的学生的概率?
(2)是否有![]() 的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)现从常喝碳酸饮料且肥胖的学生中(其中![]() 名女生),抽取
名女生),抽取![]() 人参加电视节目,则正好抽到一男一女的概率是多少?
人参加电视节目,则正好抽到一男一女的概率是多少?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式:![]() ,其中
,其中![]() )
)
参考答案:
【答案】(1)![]() (2)有
(2)有![]() 的把握(3)
的把握(3)![]()
【解析】分析:(1)肥胖的学生有![]() 人,利用古典概型的概率计算公式,即可求解概率;
人,利用古典概型的概率计算公式,即可求解概率;
(2)由已知数据利用公式求得![]() 的值,即可得到有
的值,即可得到有![]() 的把握认为肥胖与常喝碳酸饮料有关.
的把握认为肥胖与常喝碳酸饮料有关.
(3)设常喝碳酸饮料的肥胖者男生为![]() 、
、![]() 、
、![]() 、
、![]() ,女生为
,女生为![]() ,
,![]() ,得任取两人的基本事件的总数,利用古典概型的概率计算公式即可求解.
,得任取两人的基本事件的总数,利用古典概型的概率计算公式即可求解.
详解:(1)肥胖的学生有![]() 人,所以抽到肥胖的学生的概率为
人,所以抽到肥胖的学生的概率为![]() .
.
(2)由已知数据可求得:![]() .
.
因此有![]() 的把握认为肥胖与常喝碳酸饮料有关.
的把握认为肥胖与常喝碳酸饮料有关.
(3)设常喝碳酸饮料的肥胖者男生为![]() 、
、![]() 、
、![]() 、
、![]() ,女生为
,女生为![]() ,
,![]() ,则任取两人有,
,则任取两人有,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共
,共![]() 种.
种.
其中一男一女有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共8种.
,共8种.
故抽到一男一女的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在(-2,2)上的奇函数.当x∈(-2,0)时,f(x)=-loga(-x)-loga(2+x),其中a>1.
(1)求函数f(x)的零点.
(2)若t∈(0,2),判断函数f(x)在区间(0,t]上是否有最大值和最小值.若有,请求出最大值和最小值,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准
 (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过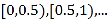 的部分按平价收费,超出
的部分按平价收费,超出 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准
 (吨),估计
(吨),估计 的值,并说明理由.
的值,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小赵和小王约定在早上
 至
至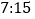 之间到某公交站搭乘公交车去上学,已知在这段时间内,共有
之间到某公交站搭乘公交车去上学,已知在这段时间内,共有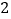 班公交车到达该站,到站的时间分别为
班公交车到达该站,到站的时间分别为 ,
,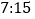 ,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 定义在
定义在 上的奇函数,且
上的奇函数,且 ,对任意
,对任意 、
、 ,
, 时,有
时,有 成立.
成立.(1)解不等式
 ;
;(2)若
 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,对称轴为
,对称轴为 ,且
,且 .
.(1)求
 的值;
的值;(2)求函数
 在
在 上的最值.
上的最值.(3)若函数
 ,且方程
,且方程 有三个解,求
有三个解,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】一古寺有一池储满了水,现一小和尚每日,按照池中所剩水一定的百分率打走一些水,且每次打水的百分率一样.10日过去,池中水恰为满池水的一半.
(1)求此百分率.(保留指数形式)
(2)若某日小和尚打完水,池中水为满池水的
 倍,小和尚已打水几日?
倍,小和尚已打水几日?(3)若某日小和尚打完水,池中水为满池水的
 倍,若古寺要求池中水不少于满池水的
倍,若古寺要求池中水不少于满池水的 ,则小和尚还能再打几日水?
,则小和尚还能再打几日水?
相关试题

