【题目】已知函数f(x)是定义在(-2,2)上的奇函数.当x∈(-2,0)时,f(x)=-loga(-x)-loga(2+x),其中a>1.
(1)求函数f(x)的零点.
(2)若t∈(0,2),判断函数f(x)在区间(0,t]上是否有最大值和最小值.若有,请求出最大值和最小值,并说明理由.
参考答案:
【答案】(1)函数f(x)的零点为-1,0,1;(2)f(x)有最大值,无最小值,理由见解析.
【解析】
(1)由奇函数![]() 在零点有意义则
在零点有意义则![]() ,然后在
,然后在![]() 上解方程
上解方程![]() ,最后利用奇函数对称性即可求出函数
,最后利用奇函数对称性即可求出函数![]() 的零点.
的零点.
(2)由奇函数的性质求出函数解析式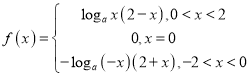 ,然后分别讨论
,然后分别讨论![]() ,和
,和![]() 时,函数
时,函数![]() 在
在![]() 上的最值.
上的最值.
(1)令-loga(-x)-loga(2+x)=0,即![]() ,
,
则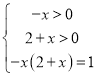 ,解得x=-1.
,解得x=-1.
由题意f(x)是定义在(-2,2)上的奇函数,∴![]() ,
,![]() ,
,
∴f(x)=0解集为{-1,0,1},故函数f(x)的零点为-1,0,1.
(2)∵f(x)是定义在(-2,2)上的奇函数,
∴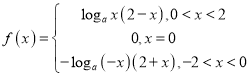
当0<t≤1时,f(x)=logax(2-x)在区间(0,t]上单调递增,
∴f(x)有最大值,f(x)max=f(t)=logat(2-t),无最小值,
当1<t<2时,f(x)=logax(2-x)在区间(0,1]上单调递增,在区间(1,t]上单调递减,∴f(x)有最大值,f(x)max=f(1)=0,无最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
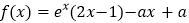 ,其中
,其中 ,若存在唯一的整数
,若存在唯一的整数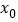 使得
使得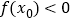 ,则
,则 的取值范围是( )
的取值范围是( )A.
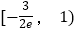 B.
B. 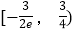 C.
C. 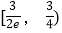 D.
D. 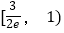
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
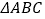 和
和 所在平面互相垂直,且
所在平面互相垂直,且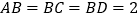 ,
, ,
, ,
, 分别为
分别为 ,
, 的中点.
的中点.
(1)求证:
 ;
;(2)求二面角
 的正弦值.
的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】平顶山市公安局交警支队依据《中华人民共和国道路交通安全法》第
 条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以
条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以 元罚款,记
元罚款,记 分的行政处罚.如表是本市一主干路段监控设备所抓拍的
分的行政处罚.如表是本市一主干路段监控设备所抓拍的 个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
个月内,机动车驾驶员不“礼让斑马线”行为统计数据:月份





违章驾驶员人数





(Ⅰ)请利用所给数据求违章人数
 与月份
与月份 之间的回归直线方程
之间的回归直线方程 ;
;(Ⅱ)预测该路段
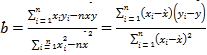 月份的不“礼让斑马线”违章驾驶员人数.
月份的不“礼让斑马线”违章驾驶员人数.参考公式:
 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准
 (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过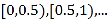 的部分按平价收费,超出
的部分按平价收费,超出 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准
 (吨),估计
(吨),估计 的值,并说明理由.
的值,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小赵和小王约定在早上
 至
至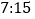 之间到某公交站搭乘公交车去上学,已知在这段时间内,共有
之间到某公交站搭乘公交车去上学,已知在这段时间内,共有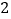 班公交车到达该站,到站的时间分别为
班公交车到达该站,到站的时间分别为 ,
,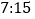 ,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对
 名六年级学生进行了问卷调查,得到如下列联表(平均每天喝
名六年级学生进行了问卷调查,得到如下列联表(平均每天喝 以上为常喝,体重超过
以上为常喝,体重超过 为肥胖):
为肥胖):常喝
不常喝
合计
肥胖



不胖



合计



(1)已知在全部
 人中随机抽取
人中随机抽取 人,求抽到肥胖的学生的概率?
人,求抽到肥胖的学生的概率?(2)是否有
 的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;(3)现从常喝碳酸饮料且肥胖的学生中(其中
 名女生),抽取
名女生),抽取 人参加电视节目,则正好抽到一男一女的概率是多少?
人参加电视节目,则正好抽到一男一女的概率是多少?











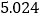


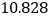
(参考公式:
 ,其中
,其中 )
)
相关试题

