【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在区间
在区间![]() 上为单调递增函数,求
上为单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() ,且
,且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() 满足条件
满足条件![]() .证明:
.证明:![]() .
.
参考答案:
【答案】(1)-1;(2)![]() ;(3)参考解析
;(3)参考解析
【解析】
试题(1)![]() ,可知
,可知![]() 在[
在[![]() ,1]是增函数,在[1,2]是减函数,所以最大值为f(1).(2)
,1]是增函数,在[1,2]是减函数,所以最大值为f(1).(2)![]() 在区间
在区间![]() 上为单调递增函数,即
上为单调递增函数,即![]() 在
在![]() 上恒成立。
上恒成立。![]() ,利用分离参数
,利用分离参数![]() 在
在![]() 上恒成立,即求
上恒成立,即求![]() 的最大值。
的最大值。
(3)![]() 有两个实根
有两个实根![]() ,
, ![]() ,两式相减
,两式相减![]() ,又
,又![]() ,
,![]()
![]() .要证:
.要证:![]() ,只需证:
,只需证:![]() ,令
,令![]() 可证。
可证。
试题解析:(1) ![]()
函数![]() 在[
在[![]() ,1]是增函数,在[1,2]是减函数,
,1]是增函数,在[1,2]是减函数,
所以![]() .
.
(2)因为![]() ,所以
,所以![]() ,
,
因为![]() 在区间
在区间![]() 单调递增函数,所以
单调递增函数,所以![]() 在(0,3)恒成立
在(0,3)恒成立
![]() ,有
,有![]() =
=![]() ,(
,(![]() )
)
综上:![]()
(3)∵![]() ,又
,又![]() 有两个实根
有两个实根![]() ,
,
∴![]() ,两式相减,得
,两式相减,得![]() ,
,
∴![]() ,
,
于是![]()
![]() .
.
![]()
要证:![]() ,只需证:
,只需证:![]()
只需证:![]() .(*)
.(*)
令![]() ,∴(*)化为
,∴(*)化为 ![]() ,只证
,只证![]() 即可.
即可.
![]() 在(0,1)上单调递增,
在(0,1)上单调递增,![]() ,
,
即![]() .∴
.∴![]() .
.
(其他解法根据情况酌情给分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,对称轴为
,对称轴为 ,且
,且 .
.(1)求
 的值;
的值;(2)求函数
 在
在 上的最值.
上的最值.(3)若函数
 ,且方程
,且方程 有三个解,求
有三个解,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】一古寺有一池储满了水,现一小和尚每日,按照池中所剩水一定的百分率打走一些水,且每次打水的百分率一样.10日过去,池中水恰为满池水的一半.
(1)求此百分率.(保留指数形式)
(2)若某日小和尚打完水,池中水为满池水的
 倍,小和尚已打水几日?
倍,小和尚已打水几日?(3)若某日小和尚打完水,池中水为满池水的
 倍,若古寺要求池中水不少于满池水的
倍,若古寺要求池中水不少于满池水的 ,则小和尚还能再打几日水?
,则小和尚还能再打几日水? -
科目: 来源: 题型:
查看答案和解析>>【题目】在某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
年份
2008
2009
2010
2011
2012
2013
2014
年份代号

1
2
3
4
5
6
7
人均纯收入

2.7
3.6
3.3
4.6
5.4
5.7
6.2
对变量
 与
与 进行相关性检验,得知
进行相关性检验,得知 与
与 之间具有线性相关关系.
之间具有线性相关关系.(1)求
 关于
关于 的线性回归方程;
的线性回归方程;(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解人们对“2019年3月在北京召开的第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议”的关注度,某部门从年龄在15岁到65岁的人群中随机调查了100人,并得到如图所示的年龄频率分布直方图,在这100人中关注度非常髙的人数与年龄的统计结果如右表所示:

年龄
关注度非常高的人数

15

5

15

23

17
(Ⅰ)由频率分布直方图,估计这100人年龄的中位数和平均数;
(Ⅱ)根据以上统计数据填写下面的
 列联表,据此表,能否在犯错误的概率不超过
列联表,据此表,能否在犯错误的概率不超过 的前提下,认为以45岁为分界点的不同人群对“两会”的关注度存在差异?
的前提下,认为以45岁为分界点的不同人群对“两会”的关注度存在差异?(Ⅲ)按照分层抽样的方法从年龄在35岁以下的人中任选六人,再从六人中随机选两人,求两人中恰有一人年龄在25岁以下的概率是多少.
45岁以下
45岁以上
总计
非常髙
一般
总计
参考数据:

0.100
0.050
0.010
0.001

2.706
3.841
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列五个结论,其中正确的结论是( )
A.函数
 的最大值为
的最大值为
B.已知函数
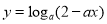 (
( 且
且 )在
)在 上是减函数则a的取值范围是
上是减函数则a的取值范围是
C.在同一直角坐标系中,函数
 与
与 的图象关于y轴对称
的图象关于y轴对称D.在同一直角坐标系中,函数
 与
与 的图象关于直线
的图象关于直线 对称
对称E.已知定义在R上的奇函数
 在
在 内有1010个零点,则函数
内有1010个零点,则函数 的零点个数为2021
的零点个数为2021 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 (
( )与抛物线
)与抛物线 (
( )共交点
)共交点 ,抛物线上的点
,抛物线上的点 到
到 轴的距离等于
轴的距离等于 ,且椭圆与抛物线的交点
,且椭圆与抛物线的交点 满足
满足 .
.(1)求抛物线的方程和椭圆的方程;
(2)国抛物线上的点
 做抛物线的切线
做抛物线的切线 交椭圆于
交椭圆于 两点,设线段
两点,设线段 的中点为
的中点为 ,求
,求 的取值范围.
的取值范围.
相关试题

