【题目】已知椭圆![]() (
(![]() )与抛物线
)与抛物线![]() (
(![]() )共交点
)共交点![]() ,抛物线上的点
,抛物线上的点![]() 到
到![]() 轴的距离等于
轴的距离等于![]() ,且椭圆与抛物线的交点
,且椭圆与抛物线的交点![]() 满足
满足![]() .
.
(1)求抛物线的方程和椭圆的方程;
(2)国抛物线上的点![]() 做抛物线的切线
做抛物线的切线![]() 交椭圆于
交椭圆于![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]()
![]() (2)
(2)![]()
【解析】
(1)根据题意及抛物线的定义可得![]() 是抛物线
是抛物线![]() 的准线,从而得到
的准线,从而得到![]() ,解得
,解得![]() 后可得方程;由题意得点
后可得方程;由题意得点![]() 的坐标为
的坐标为![]() ,然后根据椭圆的定义得到
,然后根据椭圆的定义得到![]() ,又
,又![]() ,故得
,故得![]() ,于是可得椭圆的方程.(2)由直线
,于是可得椭圆的方程.(2)由直线![]() 与抛物线相切并结合判别式可得
与抛物线相切并结合判别式可得![]() ;再根据直线与椭圆相交可得
;再根据直线与椭圆相交可得![]() ,又
,又![]() ,可得
,可得![]() .根据根与系数的关系得到
.根据根与系数的关系得到![]()
![]() .又
.又![]() ,故得
,故得![]() ,于是得到
,于是得到![]() 的取值范围是
的取值范围是![]() .
.
(1)∵抛物线上的点![]() 到
到![]() 轴的距离等于
轴的距离等于![]() ,
,
∴点![]() 到直线
到直线![]() 的距离等于点
的距离等于点![]() 到交点
到交点![]() 的距离,
的距离,
∴直线![]() 是抛物线
是抛物线![]() 的准线,
的准线,
∴![]() .
.
解得![]() ,
,
∴抛物线的方程为![]() .
.
由题意得椭圆的右焦点![]() ,左焦点
,左焦点![]() ,
,
由![]() 得
得![]() ,
,
∴![]() ,
,
又![]() ,
,
可得点![]() 的坐标为
的坐标为![]() .
.
由椭圆的定义得![]() ,
,
![]() ,
,
又![]() ,
,
∴![]() ,
,
∴椭圆的方程为![]() .
.
(2)显然![]() ,
,![]() ,
,
由![]() ,消去
,消去![]() 整理得
整理得![]() ,
,
由题意知![]() ,解得
,解得![]() .
.
由 ,消去
,消去![]() 整理得
整理得![]() ,
,
即![]() ,
,
其中![]()
![]() ,
,
∴![]() ,
,
又![]() ,得
,得![]() ,
,
解得![]() .
.
设![]() ,
,![]() ,
,
则![]() ,
,
则![]()
![]() .
.
又![]() ,
,
∴![]() .
.
∴![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,求函数
时,求函数 在
在 上的最大值;
上的最大值;(2)令
 ,若
,若 在区间
在区间 上为单调递增函数,求
上为单调递增函数,求 的取值范围;
的取值范围;(3)当
 时,函数
时,函数 的图象与
的图象与 轴交于两点
轴交于两点 ,且
,且 ,又
,又 是
是 的导函数.若正常数
的导函数.若正常数 满足条件
满足条件 .证明:
.证明: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解人们对“2019年3月在北京召开的第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议”的关注度,某部门从年龄在15岁到65岁的人群中随机调查了100人,并得到如图所示的年龄频率分布直方图,在这100人中关注度非常髙的人数与年龄的统计结果如右表所示:

年龄
关注度非常高的人数

15

5

15

23

17
(Ⅰ)由频率分布直方图,估计这100人年龄的中位数和平均数;
(Ⅱ)根据以上统计数据填写下面的
 列联表,据此表,能否在犯错误的概率不超过
列联表,据此表,能否在犯错误的概率不超过 的前提下,认为以45岁为分界点的不同人群对“两会”的关注度存在差异?
的前提下,认为以45岁为分界点的不同人群对“两会”的关注度存在差异?(Ⅲ)按照分层抽样的方法从年龄在35岁以下的人中任选六人,再从六人中随机选两人,求两人中恰有一人年龄在25岁以下的概率是多少.
45岁以下
45岁以上
总计
非常髙
一般
总计
参考数据:

0.100
0.050
0.010
0.001

2.706
3.841
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列五个结论,其中正确的结论是( )
A.函数
 的最大值为
的最大值为
B.已知函数
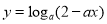 (
( 且
且 )在
)在 上是减函数则a的取值范围是
上是减函数则a的取值范围是
C.在同一直角坐标系中,函数
 与
与 的图象关于y轴对称
的图象关于y轴对称D.在同一直角坐标系中,函数
 与
与 的图象关于直线
的图象关于直线 对称
对称E.已知定义在R上的奇函数
 在
在 内有1010个零点,则函数
内有1010个零点,则函数 的零点个数为2021
的零点个数为2021 -
科目: 来源: 题型:
查看答案和解析>>【题目】某种热饮需用开水冲泡,其基本操作流程如下:①先将水加热到100
 ,水温
,水温 与时间
与时间 近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度
近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度 与时间
与时间 近似满足函数的关系式为
近似满足函数的关系式为  (
( 为常数), 通常这种热饮在40
为常数), 通常这种热饮在40 时,口感最佳,某天室温为
时,口感最佳,某天室温为 时,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为
时,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为
A. 35
 B. 30
B. 30
C. 25
 D. 20
D. 20
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知幂函数
 在
在 上单调递增,又函数
上单调递增,又函数 .
.(1)求实数
 的值,并说明函数
的值,并说明函数 的单调性;
的单调性;(2)若不等式
 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
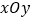 中,直线
中,直线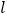 经过点
经过点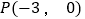 ,其倾斜角为
,其倾斜角为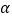 ,以原点
,以原点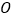 为极点,以
为极点,以 轴为非负半轴为极轴,与坐标系
轴为非负半轴为极轴,与坐标系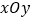 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线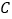 的极坐标方程为
的极坐标方程为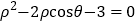 .
.(1)若直线
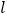 与曲线
与曲线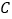 有公共点,求倾斜角
有公共点,求倾斜角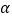 的取值范围;
的取值范围;(2)设
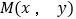 为曲线
为曲线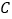 上任意一点,求
上任意一点,求 的取值范围.
的取值范围.
相关试题

