【题目】已知定义域为![]() 的单调递减的奇函数
的单调递减的奇函数![]() ,当
,当![]() 时,
时, ![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)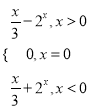 ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据函数为奇函数得![]() ,结合当
,结合当![]() 时,
时, ![]() ,即可求出
,即可求出![]() 的值;(2)由定义域为
的值;(2)由定义域为![]() 的函数
的函数![]() 是奇函数,知
是奇函数,知![]() .当
.当![]() 时,
时, ![]() ,由函数
,由函数![]() 是奇函数,知
是奇函数,知![]() ,由此能求出
,由此能求出![]() 的解析式;(3)由
的解析式;(3)由![]() 是
是![]() 上单调递减的奇函数,
上单调递减的奇函数, ![]() ,得
,得![]() 即
即![]() 恒成立,再由根的判别式小于零即可求出实数
恒成立,再由根的判别式小于零即可求出实数![]() 的取值范围.
的取值范围.
试题解析:(1)f(﹣1)=﹣f(1)=﹣(![]() ﹣2)=
﹣2)=![]() ;
;
(2)∵定义域为R的函数f(x)是奇函数,
∴f(0)=0,
当x<0时,﹣x>0,
f(﹣x)=﹣![]() ﹣2﹣x ,
﹣2﹣x ,
又∵函数f(x)是奇函数,
∴f(﹣x)=﹣f(x),
∴f(x)=![]() +2﹣x ,
+2﹣x ,
综上所述f(x)=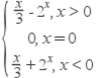 .
.
(3)∵f(1)=﹣![]() <f(0)=0,
<f(0)=0,
且f(x)在R上单调,
∴f(x)在R上单调递减,
由f(t2﹣2t)+f(2t2﹣k)<0,
得f(t2﹣2t)<﹣f(2t2﹣k),
∵f(x)是奇函数,
∴f(t2﹣2t)<f(k﹣2t2),
又∵f(x)是减函数,
∴t2﹣2t>k﹣2t2
即3t2﹣2t﹣k>0对任意t∈R恒成立,
∴△=4+12k<0得k<﹣![]() ,即为所求.
,即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下的对应数据:
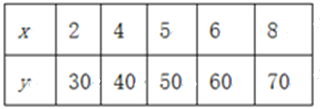
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 =
=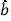 x+
x+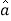 ;
;(参考公式:用最小二乘法求线性回归方程系数公式
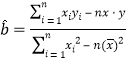 ,
,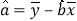 .)
.) -
科目: 来源: 题型:
查看答案和解析>>【题目】在
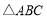 中,角
中,角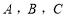 所对的边分别为
所对的边分别为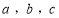 ,且
,且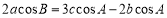 .
.(1)若
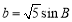 ,求
,求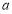 ;
;(2)若
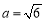 ,
,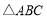 的面积为
的面积为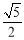 ,求
,求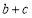 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等式:sin25°+cos235°+sin 5°cos 35°=
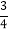 ,
,sin215°+cos245°+sin 15°cos 45°=
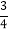 ,sin230°+cos260°+sin 30°·cos 60°=
,sin230°+cos260°+sin 30°·cos 60°=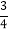 ,…,由此归纳出对任意角度θ都成立的一个等式,并予以证明.
,…,由此归纳出对任意角度θ都成立的一个等式,并予以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:函数
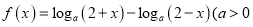 且
且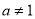 .
. (1)求
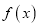 定义域;
定义域;(2)判断
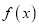 的奇偶性,并说明理由;
的奇偶性,并说明理由;(3)求使
 的
的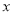 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
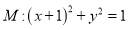 ,圆
,圆 ,动圆
,动圆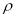 与圆
与圆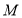 外切并与圆
外切并与圆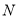 内切,圆心
内切,圆心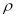 的轨迹为曲线
的轨迹为曲线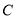 .
.(1)求
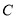 的方程;
的方程;(2)
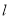 是与圆
是与圆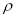 ,圆
,圆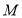 都相切的一条直线,
都相切的一条直线,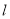 与曲线
与曲线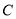 交于
交于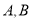 两点,当圆
两点,当圆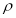 的半径最长时,求
的半径最长时,求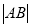 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(1)若函数
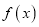 的值域为
的值域为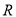 ,求实数
,求实数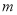 的取值范围;
的取值范围;(2)若函数
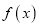 在区间
在区间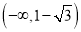 上是减函数,求实数
上是减函数,求实数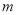 的取值范围.
的取值范围.
相关试题

