【题目】已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并与圆
外切并与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程;
的方程;
(2)![]() 是与圆
是与圆![]() ,圆
,圆![]() 都相切的一条直线,
都相切的一条直线,![]() 与曲线
与曲线![]() 交于
交于![]() 两点,当圆
两点,当圆![]() 的半径最长时,求
的半径最长时,求![]() .
.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() .
.
【解析】
试题分析:对于(1),圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() ,圆
,圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() ,设圆
,设圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,由已知条件不难得到
,由已知条件不难得到![]() ,进而可得曲线
,进而可得曲线![]() 是以
是以![]() 为左、右焦点,长半轴长为
为左、右焦点,长半轴长为![]() ,短半轴长为
,短半轴长为![]() 的椭圆,据此即可求出其方程;对于(2),首先根据已知条件圆
的椭圆,据此即可求出其方程;对于(2),首先根据已知条件圆![]() 的方程,接下来需要分直线
的方程,接下来需要分直线![]() 的斜率存在与不存在两种情况,并结合点到直线的距离公式和弦长公式进行解答即可.
的斜率存在与不存在两种情况,并结合点到直线的距离公式和弦长公式进行解答即可.
试题解析:由已知得圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() ;圆
;圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() ,设圆
,设圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() .
.
(1)因为圆![]() 与圆
与圆![]() 外切并且与圆
外切并且与圆![]() 内切,所以
内切,所以
![]() .
.
由椭圆的定义可知,曲线![]() 是以
是以![]() 为左、右焦点,长半轴长为
为左、右焦点,长半轴长为![]() ,短半轴长为
,短半轴长为![]() 的椭圆(左顶点除外),其方程为
的椭圆(左顶点除外),其方程为![]() .……5分
.……5分
(2)对于曲线![]() 上任意一点
上任意一点![]() ,由于
,由于![]() ,所以
,所以![]() ,当且仅当圆
,当且仅当圆![]() 的圆心为
的圆心为![]() 时,
时,![]() .所以当圆
.所以当圆![]() 的半径最长时,其方程为
的半径最长时,其方程为
![]() .
.
若![]() 的倾斜角为
的倾斜角为![]() ,则
,则![]() 与
与![]() 轴重合,可得
轴重合,可得![]() .
.
若![]() 的倾斜角不为
的倾斜角不为![]() ,由
,由![]() 知
知![]() 不平行于
不平行于![]() 轴,设
轴,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,
则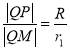 ,可求得
,可求得![]() ,所以可设
,所以可设![]() .由
.由![]() 与圆
与圆![]() 相切得
相切得![]() ,解得
,解得![]() .
.
当![]() 时,将
时,将![]() 带入
带入![]() ,并整理得
,并整理得![]() ,
,
解得![]() .所以
.所以![]() .
.
当![]() 时,由图形的对称性可知
时,由图形的对称性可知![]() .综上,
.综上,![]() 或
或![]() .……12分
.……12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等式:sin25°+cos235°+sin 5°cos 35°=
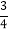 ,
,sin215°+cos245°+sin 15°cos 45°=
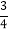 ,sin230°+cos260°+sin 30°·cos 60°=
,sin230°+cos260°+sin 30°·cos 60°=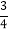 ,…,由此归纳出对任意角度θ都成立的一个等式,并予以证明.
,…,由此归纳出对任意角度θ都成立的一个等式,并予以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为
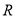 的单调递减的奇函数
的单调递减的奇函数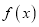 ,当
,当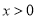 时,
时, 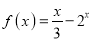 .
.(1)求
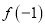 的值;
的值;(2)求
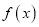 的解析式;
的解析式;(3)若对任意的
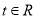 ,不等式
,不等式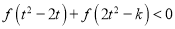 恒成立,求实数
恒成立,求实数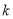 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:函数
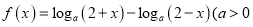 且
且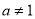 .
. (1)求
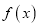 定义域;
定义域;(2)判断
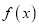 的奇偶性,并说明理由;
的奇偶性,并说明理由;(3)求使
 的
的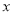 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(1)若函数
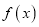 的值域为
的值域为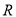 ,求实数
,求实数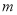 的取值范围;
的取值范围;(2)若函数
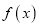 在区间
在区间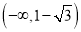 上是减函数,求实数
上是减函数,求实数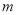 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数h(x)=(m2-5m+1)xm+1为幂函数,且为奇函数.
(I)求m的值;
(II)求函数g(x)=h(x)+
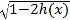 ,x∈
,x∈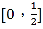 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
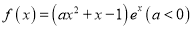 .
.(1)当
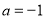 时,函数
时,函数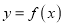 与
与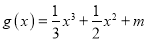 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数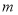 的范围;
的范围;(2)讨论
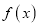 的单调性.
的单调性.
相关试题

