【题目】给出下列命题:
①纯虚数z的共轭复数是![]() ;
;
②若![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() 与
与![]() 互为共轭复数;
互为共轭复数;
④若![]() ,则
,则![]() 与
与![]() 互为共轭复数.
互为共轭复数.
其中正确命题的序号是_________.
参考答案:
【答案】①④
【解析】
对于①,根据纯虚数和共轭复数的定义可知正确;对于②,由![]() 得出
得出![]() ,再由复数相等和共轭复数的定义,可知不一定有
,再由复数相等和共轭复数的定义,可知不一定有![]() ,可知②不正确;对于③,
,可知②不正确;对于③,![]() ,则
,则![]() 可能均为实数,但不一定相等,或
可能均为实数,但不一定相等,或![]() 与
与![]() 的虚部互为相反数,但实部不一定相等,
的虚部互为相反数,但实部不一定相等,
,即可判断出③;对于④,由![]() 得出
得出![]() ,则
,则![]() 与
与![]() 互为共轭复数,则④正确;综合得出答案.
互为共轭复数,则④正确;综合得出答案.
解:根据纯虚数和共轭复数的定义,可知命题①显然正确;
对于②,若![]() ,只能得到
,只能得到![]() ,不一定有
,不一定有![]() ,所以命题②不正确;
,所以命题②不正确;
对于③,若![]() ,则
,则![]() 可能均为实数,但不一定相等,
可能均为实数,但不一定相等,
或![]() 与
与![]() 的虚部互为相反数,但实部不一定相等,
的虚部互为相反数,但实部不一定相等,
则![]() 与
与![]() 不一定互为共轭复数,所以命题③不正确;
不一定互为共轭复数,所以命题③不正确;
由![]() 得出
得出![]() ,则
,则![]() 与
与![]() 互为共轭复数,可知命题④正确;
互为共轭复数,可知命题④正确;
所以正确命题的序号是①④.
故答案为:①④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,若
中,若 ,则这三角形一定是( )
,则这三角形一定是( )A. 等腰三角形 B. 直角三角形 C. 等腰直角三角形 D. 等腰或直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(
 ,
, )
)C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程
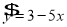 ,变量x增加一个单位时,y平均增加5个单位;
,变量x增加一个单位时,y平均增加5个单位;③线性回归方程
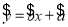 必过
必过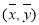 ;
;④在一个
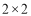 列联表中,由计算得是
列联表中,由计算得是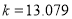 ,则有
,则有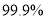 的把握确认这两个变量间有关系.
的把握确认这两个变量间有关系.其中错误的个数是( )
本题可以参考独立性检验临界值表:
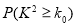
0.05
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
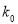
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
A.0B.1C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四面体
 中,
中, ,则四面体体积最大时,它的外接球半径
,则四面体体积最大时,它的外接球半径 _________.
_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四棱锥
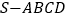 中,
中,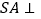 底面
底面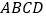 ,
,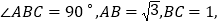
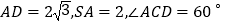 ,
, 为
为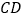 的中点.
的中点. 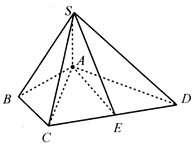
(1)求证:
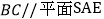 ;
;(2)求点D与平面
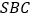 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品
不喜欢甜品
合计
南方学生
60
20
80
北方学生
10
10
20
合计
70
30
100
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品.现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
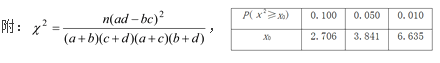
相关试题

