【题目】在四面体![]() 中,
中,![]() ,则四面体体积最大时,它的外接球半径
,则四面体体积最大时,它的外接球半径![]() _________.
_________.
参考答案:
【答案】![]()
【解析】
由题意画出图形,取AB中点E,连接CE,DE,设AB=2x(0<x<1),则CE=DE=![]() ,可知当平面ABC⊥平面ABD时,四面体体积最大,写出体积公式,利用导数求得体积最大时的x值,再由△ABD的外心G与△ABC的外心H作两个三角形所在平面的垂线,可得交点O为四面体ABCD的外接球的球心,然后求解三角形得答案.
,可知当平面ABC⊥平面ABD时,四面体体积最大,写出体积公式,利用导数求得体积最大时的x值,再由△ABD的外心G与△ABC的外心H作两个三角形所在平面的垂线,可得交点O为四面体ABCD的外接球的球心,然后求解三角形得答案.
如图,

取AB中点E,连接CE,DE,
设AB=2x(0<x<1),则CE=DE=![]() ,
,
∴当平面ABC⊥平面ABD时,四面体体积最大,
为V=![]() =
=![]() =
=![]() .
.
V′=![]() ,当x∈(0,
,当x∈(0,![]() )时,V为增函数,当x∈(
)时,V为增函数,当x∈(![]() ,1)时,V为减函数,
,1)时,V为减函数,
则当x=![]() 时,V有最大值.
时,V有最大值.
设△ABD的外心为G,△ABC的外心为H,
分别过G、H作平面ABD、平面ABC的垂线交于O,则O为四面体ABCD的外接球的球心.
在△ABD中,有sin![]() ,则cos
,则cos![]() ,
,
∴sin![]() =
=![]() .
.
设△ABD的外接圆的半径为r,则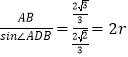 ,即DG=r=
,即DG=r=![]() .
.
又DE=![]() ,∴OG=HE=GE=
,∴OG=HE=GE=![]() .
.
∴它的外接球半径R=OD=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年
 月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在
月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在 岁之间的
岁之间的 人进行调查,经统计“年轻人”与“中老年人”的人数之比为
人进行调查,经统计“年轻人”与“中老年人”的人数之比为 .
.关注
不关注
合计
年轻人

中老年人
合计



(1)根据已知条件完成上面的
 列联表,并判断能否有
列联表,并判断能否有 的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?
的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?(2)现已用分层抽样的办法从中老年人中选取了
 人进行问卷调查.若再从这
人进行问卷调查.若再从这 人中选取
人中选取 人进行面对面询问,求事件“选取的
人进行面对面询问,求事件“选取的 人中恰有
人中恰有 人关注“中国湖北(潜江)龙虾节””的概率.
人关注“中国湖北(潜江)龙虾节””的概率.附:参考公式
 ,其中
,其中 .
.临界值表:






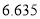

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
 中,底面
中,底面 为平行四边形,点
为平行四边形,点 、
、 、
、 分别在
分别在 、
、 、
、 上.
上.
(1)若
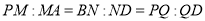 ,求证:平面
,求证:平面 平面
平面 ;
;(2)若
 满足
满足 ,则
,则 点满足什么条件时,
点满足什么条件时, 面
面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】过点
 作抛物线
作抛物线 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,
, ,
, 分别交
分别交 轴于
轴于 ,
, 两点,
两点, 为坐标原点,则
为坐标原点,则 与
与 的面积之比为( )
的面积之比为( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 在
在 上有定义,要使函数
上有定义,要使函数 有定义,则a的取值范围为
有定义,则a的取值范围为A.
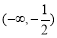 ;B.
;B. C.
C. ;D.
;D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,且
,且 .
. 求定义域;
求定义域; 若函数
若函数 的反函数是其本身,求a的值;
的反函数是其本身,求a的值; 求函数
求函数 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 是圆心为
是圆心为 半径为
半径为 的半圆弧上从点
的半圆弧上从点 数起的第一个三等分点,点
数起的第一个三等分点,点 是圆心为
是圆心为 半径为
半径为 的半圆弧的中点,
的半圆弧的中点, 、
、 分别是两个半圆的直径,
分别是两个半圆的直径, ,直线
,直线 与两个半圆所在的平面均垂直,直线
与两个半圆所在的平面均垂直,直线 、
、 共面.
共面.
(1)求三棱锥
 的体积;
的体积;(2)求直线
 与
与 所成角的余弦值.
所成角的余弦值.
相关试题

