【题目】已知椭圆G:![]() ,过点A(0,5),B(﹣8,﹣3),C、D在该椭圆上,直线CD过原点O,且在线段AB的右下侧.
,过点A(0,5),B(﹣8,﹣3),C、D在该椭圆上,直线CD过原点O,且在线段AB的右下侧.
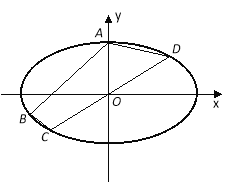
(1)求椭圆G的方程;
(2)求四边形ABCD 的面积的最大值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题分析:(1)先将点A(0,5),B(-8,3),代入椭圆的方程解得:a=10 b=5,最后写出椭圆G的方程;(2)连OB,则四边形ABCD的面积![]() ,
,![]() 分别表示A,B到直线CD的距离,设CD:-kx+y=0,代入椭圆方程消去y得到关于x的一元二次方程,再结合求根公式即可求得四边形ABCD的面积,最后结合基本不等式求最大值,从而解决问题
分别表示A,B到直线CD的距离,设CD:-kx+y=0,代入椭圆方程消去y得到关于x的一元二次方程,再结合求根公式即可求得四边形ABCD的面积,最后结合基本不等式求最大值,从而解决问题
试题解析:(1)将点A(0,5),B(﹣8,﹣3)代入椭圆G 的方程解得:
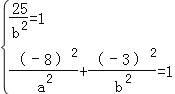 ,解得:a2=100,b2=25.
,解得:a2=100,b2=25.
∴椭圆G的方程为:![]() ;
;
(2)连结OB,
则![]() ,---7分
,---7分
其中dA,dB分别表示点A,点B 到直线CD 的距离.
设直线CD方程为y =kx,代入椭圆方程![]() ,得x2+4k2x2﹣100=0,
,得x2+4k2x2﹣100=0,
解得:![]() ,
,
∴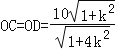 ,
,
又![]() ,
,![]() ,
,
则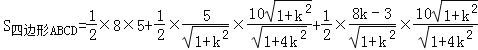
=![]() .
.
当且仅当k=1时 取等号。
-
科目: 来源: 题型:
查看答案和解析>>【题目】四棱锥P﹣ABCD中,底面ABCD是边长为8的菱形,∠BAD=
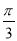 ,若PA=PD=5,平面PAD⊥平面ABCD.
,若PA=PD=5,平面PAD⊥平面ABCD.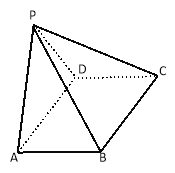
(1)求四棱锥P﹣ABCD的体积;
(2)求证:AD⊥PB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,四边形ADEF是正方形,且BD⊥平面CDE,H是BE的中点,G是AE,DF的交点.

(1)求证:GH∥平面CDE;
(2)求证:面ADEF⊥面ABCD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营一批进价为
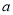 元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:
元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:销售价(
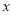 元/台)
元/台)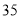
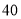
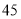
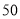
日销售量(
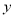 台)
台)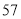
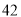
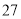
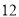
日销售额(
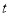 元)
元)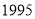
日销售利润(
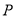 元)
元)
(1)在下面给出的直角坐标系中,根据表中的数据描出实数对
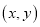 的对应点,并写出
的对应点,并写出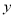 与
与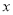 的一个函数关系式;
的一个函数关系式;
(2)请把表中的空格里的数据填上;
(3)根据表中的数据求
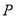 与
与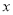 的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?
的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,设△ABC的顶点分别为
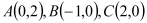 ,圆M是△ABC的外接圆,直线
,圆M是△ABC的外接圆,直线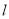 的方程是
的方程是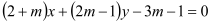 ,
,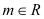
(1)求圆M的方程;
(2)证明:直线
 与圆M相交;
与圆M相交;(3)若直线
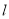 被圆M截得的弦长为3,求直线
被圆M截得的弦长为3,求直线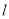 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
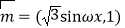 ,
,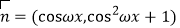 ,设函数
,设函数 .
.(1)若函数
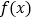 的图象关于直线
的图象关于直线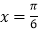 对称,且
对称,且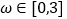 时,求函数
时,求函数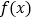 的单调增区间;
的单调增区间;(2)在(1)的条件下,当
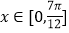 时,函数
时,函数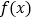 有且只有一个零点,求实数
有且只有一个零点,求实数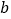 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前
的前 项和为
项和为 ,且满足
,且满足 ,求数列
,求数列 的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.思路1:先设
 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出 _________,
_________,  __________,
__________,  _________.
_________.猜想:
 _______.
_______.然后用数学归纳法证明.证明过程如下:
①当
 时,________________,猜想成立
时,________________,猜想成立②假设
 (
( N*)时,猜想成立,即
N*)时,猜想成立,即 _______.
_______.那么,当
 时,由已知
时,由已知 ,得
,得 _________.
_________.又
 ,两式相减并化简,得
,两式相减并化简,得 _____________(用含
_____________(用含 的代数式表示).
的代数式表示).所以,当
 时,猜想也成立.
时,猜想也成立.根据①和②,可知猜想对任何
 N*都成立.
N*都成立.思路2:先设
 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出 _____________.
_____________.由已知
 ,写出
,写出 与
与 的关系式:
的关系式:  _____________________,
_____________________,两式相减,得
 与
与 的递推关系式:
的递推关系式:  ____________________.
____________________.整理:
 ____________.
____________.发现:数列
 是首项为________,公比为_______的等比数列.
是首项为________,公比为_______的等比数列.得出:数列
 的通项公式
的通项公式 ____,进而得到
____,进而得到 ____________.
____________.
相关试题

