【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为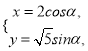 (
(![]() 为参数),以直角坐标系原点
为参数),以直角坐标系原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值及其对应的点
距离的最大值及其对应的点![]() 的直角坐标.
的直角坐标.
参考答案:
【答案】(Ⅰ) 曲线![]() 的普通方程为:
的普通方程为: ![]() ,直线
,直线![]() 的直角坐标方程为
的直角坐标方程为![]() . (Ⅱ) 最大值为
. (Ⅱ) 最大值为![]() , 点
, 点![]() 的坐标为
的坐标为![]() .
.
【解析】试题分析:
(1)消去参数可曲线![]() 的普通方程为:
的普通方程为: ![]() ,极坐标化简直角坐标可得直线
,极坐标化简直角坐标可得直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)利用点到直线距离公式可得![]() ,由三角函数的 性质可得
,由三角函数的 性质可得![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() .
.
试题解析:
(Ⅰ)曲线![]() 的普通方程为:
的普通方程为: ![]() ,
,
![]() 化简为
化简为![]() ,
,
∴直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,
,
则点![]() 到直线
到直线![]() 的距离
的距离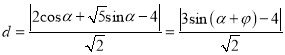 ,
,
其中![]() .
.
显然当![]() 时,
时, ![]() ,
,
此时![]() ,
,
∴![]() ,
,
![]() ,
,
即点![]() 的坐标为
的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (m∈Z)为偶函数,且在(0,+∞)上为增函数.
(m∈Z)为偶函数,且在(0,+∞)上为增函数.
(1)求m的值,并确定f(x)的解析式;
(2)若g(x)=loga[f(x)﹣ax](a>0且a≠1),是否存在实数a,使g(x)在区间[2,3]上的最大值为2,若存在,求出a的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】连掷一枚均匀的骰子两次,所得向上的点数分别为
 ,记
,记 ,则下列说法正确的是( )
,则下列说法正确的是( )A. 事件“
 ”的概率为
”的概率为 B. 事件“
B. 事件“ 是奇数”与“
是奇数”与“ ”互为对立事件
”互为对立事件C. 事件“
 ”与“
”与“ ”互为互斥事件 D. 事件“
”互为互斥事件 D. 事件“ ”的概率为
”的概率为
-
科目: 来源: 题型:
查看答案和解析>>【题目】A={x|x2﹣2x﹣8<0},B={x|x2+2x﹣3>0},C={x|x2﹣3ax+2a2<0},
(1)求A∩B.
(2)试求实数a的取值范围,使C(A∩B). -
科目: 来源: 题型:
查看答案和解析>>【题目】四名同学根据各自的样本数据研究变量
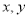 之间的相关关系,并求得回归直线方程,分别得到以下四个结论:( )
之间的相关关系,并求得回归直线方程,分别得到以下四个结论:( )①
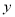 与
与 负相关且
负相关且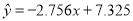 . ②
. ②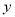 与
与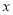 负相关且
负相关且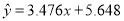
③
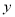 与
与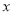 正相关且
正相关且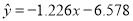 ④
④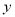 与
与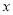 正相关且
正相关且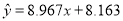
其中正确的结论的序号是( )
A. ①② B. ②③ C. ①④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
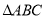 中,
中, 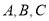 成等差数列是
成等差数列是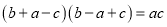 的( )
的( )A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在原点
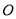 ,焦点在
,焦点在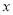 轴上的椭圆
轴上的椭圆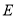 过点
过点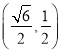 ,离心率为
,离心率为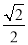 .
.(1)求椭圆
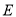 的方程;
的方程;(2)直线
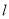 过椭圆
过椭圆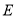 的左焦点
的左焦点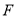 ,且与椭圆
,且与椭圆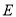 交于
交于 两点,若
两点,若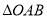 的面积为
的面积为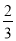 ,求直线
,求直线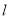 的方程.
的方程.
相关试题

