【题目】连掷一枚均匀的骰子两次,所得向上的点数分别为![]() ,记
,记![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 事件“![]() ”的概率为
”的概率为![]() B. 事件“
B. 事件“![]() 是奇数”与“
是奇数”与“![]() ”互为对立事件
”互为对立事件
C. 事件“![]() ”与“
”与“![]() ”互为互斥事件 D. 事件“
”互为互斥事件 D. 事件“![]() ”的概率为
”的概率为![]()
参考答案:
【答案】D
【解析】对于A, ![]() ,则概率为
,则概率为![]() ,选项错误;
,选项错误;
对于B, “![]() 是奇数”即向上的点数为奇数与偶数之和,其对立事件为都是奇数或都是偶数,选项错误;
是奇数”即向上的点数为奇数与偶数之和,其对立事件为都是奇数或都是偶数,选项错误;
对于C,事件“![]() ”包含在“
”包含在“![]() ”中,不为互斥事件,选项错误;
”中,不为互斥事件,选项错误;
对于D, 事件“![]() ”的点数有:
”的点数有: ![]() ,共9种,故概率为
,共9种,故概率为![]() ,选项正确;
,选项正确;
综上可得,选D.
点睛:事件A和B的交集为空,A与B就是互斥事件,也可以描述为:不可能同时发生的事件,则事件A与事件B互斥,从集合的角度即![]() ;若A交B为不可能事件,A并B为必然事件,那么事件A与事件B互为对立事件,即事件A与事件B在一次试验中有且仅有一个发生,其定义为:其中必有一个发生的两个互斥事件为对立事件.
;若A交B为不可能事件,A并B为必然事件,那么事件A与事件B互为对立事件,即事件A与事件B在一次试验中有且仅有一个发生,其定义为:其中必有一个发生的两个互斥事件为对立事件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
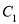 :
: 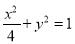 ,曲线
,曲线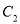 上的动点
上的动点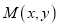 满足:
满足: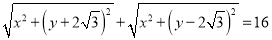 .
.(1)求曲线
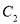 的方程;
的方程;(2)设
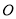 为坐标原点,第一象限的点
为坐标原点,第一象限的点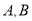 分别在
分别在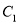 和
和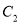 上,
上, 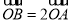 ,求线段
,求线段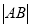 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=log4(4x+1)+2kx(k∈R)是偶函数.
(1)求k的值;
(2)若方程f(x)=m有解,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (m∈Z)为偶函数,且在(0,+∞)上为增函数.
(m∈Z)为偶函数,且在(0,+∞)上为增函数.
(1)求m的值,并确定f(x)的解析式;
(2)若g(x)=loga[f(x)﹣ax](a>0且a≠1),是否存在实数a,使g(x)在区间[2,3]上的最大值为2,若存在,求出a的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】A={x|x2﹣2x﹣8<0},B={x|x2+2x﹣3>0},C={x|x2﹣3ax+2a2<0},
(1)求A∩B.
(2)试求实数a的取值范围,使C(A∩B). -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
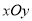 中,已知曲线
中,已知曲线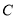 的参数方程为
的参数方程为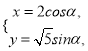 (
(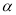 为参数),以直角坐标系原点
为参数),以直角坐标系原点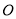 为极点,
为极点, 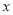 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线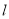 的极坐标方程为
的极坐标方程为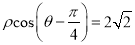 .
.(Ⅰ)求曲线
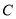 的普通方程与直线
的普通方程与直线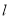 的直角坐标方程;
的直角坐标方程;(Ⅱ)设点
 为曲线
为曲线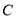 上的动点,求点
上的动点,求点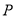 到直线
到直线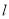 距离的最大值及其对应的点
距离的最大值及其对应的点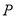 的直角坐标.
的直角坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】四名同学根据各自的样本数据研究变量
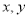 之间的相关关系,并求得回归直线方程,分别得到以下四个结论:( )
之间的相关关系,并求得回归直线方程,分别得到以下四个结论:( )①
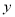 与
与 负相关且
负相关且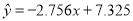 . ②
. ②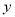 与
与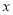 负相关且
负相关且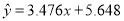
③
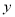 与
与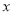 正相关且
正相关且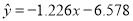 ④
④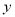 与
与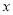 正相关且
正相关且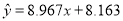
其中正确的结论的序号是( )
A. ①② B. ②③ C. ①④ D. ③④
相关试题

