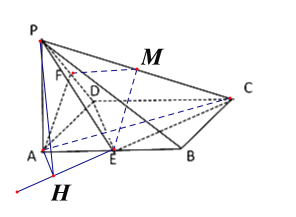
【题目】已知在四棱锥中，底面是矩形，平面，，分别是，的中点，与平面所成的角的正切值是；

（1）求证：平面；

（2）求二面角的正切值．

【答案】(1)见证明；(2)

【解析】

（1）取的中点，连接，通过证明四边形是平行四边形，证得，从而证得平面.（2）连接，证得为与平面所成角.根据的值求得的长，作出二面角的平面角并证明，解直角三角形求得二面角的正切值．

（1）证明：取的中点，连接.∵是中点

∴

又是的中点,∴

∴，从而四边形是平行四边形， 故

又平面，平面，∴

（2）∵平面，∴是在平面内的射影

为与平面所成角，

四边形为矩形，

∵,∴,

∴

过点作交的延长线于，连接，

∵平面

据三垂线定理知.∴是二面角的平面角

易知道为等腰直角三角形，∴

∴=

∴二面角的正切值为

关闭