【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表: 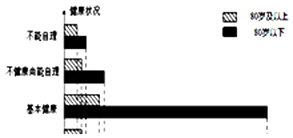
(1)若采取分层抽样的方法再从样本中的不能自理的老人中抽取16人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发 放生活补贴,标准如下:①80岁及以上长者每人每月发放生活补贴200元;②80岁以下 老人每人每月发放生活补贴120元;③不能自理的老人每人每月额外发放生活补贴100 元.试估计政府执行此计划的年度预算.
参考答案:
【答案】
(1)解:数据整理如下表:
健康状况 | 健康 | 基本健康 | 不健康尚能自理 | 不能自理 |
80岁及以上 | 20 | 45 | 20 | 15 |
80岁以下 | 200 | 225 | 50 | 25 |
从图表中知不能自理的80岁及以上长者占比为: ![]() =
= ![]() ,
,
故抽取16人中不能自理的80岁及以上长者人数为16× ![]() =6.80岁以下长者人数为10人
=6.80岁以下长者人数为10人
(2)解:在600人中80岁及以上长者在老人中占比为: ![]() =
= ![]() ,
,
用样本估计总体,80岁及以上长者共有 ![]() 万,
万,
80岁及以上长者占户籍人口的百分比为 ![]() 100%=2.75%
100%=2.75%
(3)解:用样本估计总体,设任一户籍老人每月享受的生活补助为X元,
P(X=0)= ![]() ,P(X=120)=
,P(X=120)= ![]() ×
× ![]() =
= ![]() ,P(X=200)=
,P(X=200)= ![]() =
= ![]() ,
,
P(X=220)= ![]() =
= ![]() ,P(X=300)=
,P(X=300)= ![]() =
= ![]() ,
,
则随机变量X的分布列为:
X | 0 | 120 | 220 | 300 | |
P |
|
|
|
|
|
EX=0× ![]() +120×
+120× ![]() +200×
+200× ![]() +220×
+220× ![]() +300×
+300× ![]() =28,
=28,
全市老人的总预算为28×12×66×104=2.2176×108元.
政府执行此计划的年度预算约为2.2176亿元
【解析】(Ⅰ)数据整理如下表:
健康状况 | 健康 | 基本健康 | 不健康尚能自理 | 不能自理 |
80岁及以上 | 20 | 45 | 20 | 15 |
80岁以下 | 200 | 225 | 50 | 25 |
利用频率计算公式即可得出.(Ⅱ)在600人中80岁及以上长者在老人中占比为: ![]() ,用样本估计总体,80岁及以上长者共有
,用样本估计总体,80岁及以上长者共有 ![]() 万,即可得出80岁及以上长者占户籍人口的百分比.(Ⅲ)用样本估计总体,设任一户籍老人每月享受的生活补助为X元,P(X=0)=
万,即可得出80岁及以上长者占户籍人口的百分比.(Ⅲ)用样本估计总体,设任一户籍老人每月享受的生活补助为X元,P(X=0)= ![]() ,P(X=120)=
,P(X=120)= ![]() ×
× ![]() ,P(X=200)=
,P(X=200)= ![]() ,P(X=220)=
,P(X=220)= ![]() ,P(X=300)=
,P(X=300)= ![]() ,及其数学期望.
,及其数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为F1(-c,0),F2(c,0),直线
的左、右焦点分别为F1(-c,0),F2(c,0),直线 交椭圆E于A,B两点,△ABF1的周长为16,△AF1F2的周长为12.
交椭圆E于A,B两点,△ABF1的周长为16,△AF1F2的周长为12.(1)求椭圆E的标准方程与离心率;
(2)若直线l与椭圆E交于C,D两点,且P(2,2)是线段CD的中点,求直线l的一般方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直三棱柱ABC﹣A1B1C1的底面为正三角形,E,F分别是A1C1 , B1C1上的点,且满足A1E=EC1 , B1F=3FC1 .
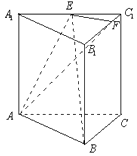
(1)求证:平面AEF⊥平面BB1C1C;
(2)设直三棱柱ABC﹣A1B1C1的棱长均相等,求二面角C1﹣AE﹣B的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
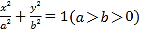 的右顶点为A,上顶点为B.已知椭圆的离心率为
的右顶点为A,上顶点为B.已知椭圆的离心率为 ,
, .
.(1)求椭圆的方程;
(2)设直线
 与椭圆交于
与椭圆交于 ,
, 两点,
两点, 与直线
与直线 交于点M,且点P,M均在第四象限.若
交于点M,且点P,M均在第四象限.若 的面积是
的面积是 面积的2倍,求
面积的2倍,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在原点的双曲线
 的右焦点为
的右焦点为 ,右顶点为
,右顶点为 .
.(1)求双曲线
 的方程;
的方程;(2)若直线
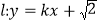 与双曲线
与双曲线 恒有两个不同的交点
恒有两个不同的交点 和
和 ,且
,且 (其中
(其中 为坐标原点),求实数
为坐标原点),求实数 取值范围.
取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,设椭圆
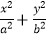 =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.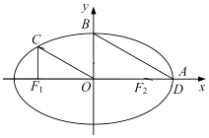
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ≤e≤
≤e≤ 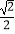 ,求
,求 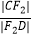 的取值范围.
的取值范围.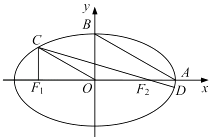
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xe2x﹣lnx﹣ax.
(1)当a=0时,求函数f(x)在[ ,1]上的最小值;
,1]上的最小值;
(2)若x>0,不等式f(x)≥1恒成立,求a的取值范围;
(3)若x>0,不等式f(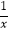 )﹣1≥
)﹣1≥ 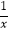 e
e  +
+ 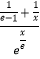 恒成立,求a的取值范围.
恒成立,求a的取值范围.
相关试题

