【题目】设函数f(x)=1﹣ ![]() ,g(x)=ln(ax2﹣3x+1),若对任意的x1∈[0,+∞),都存在x2∈R,使得f(x1)=g(x2)成立,则实数a的最大值为( )
,g(x)=ln(ax2﹣3x+1),若对任意的x1∈[0,+∞),都存在x2∈R,使得f(x1)=g(x2)成立,则实数a的最大值为( )
A.2
B.![]()
C.4
D.![]()
参考答案:
【答案】B
【解析】解:设g(x)=ln(ax2﹣3x+1)的值域为A,
∵f(x)=1﹣ ![]() 在[0,+∞)上的值域为(﹣∞,0],
在[0,+∞)上的值域为(﹣∞,0],
∴(﹣∞,0]A,
∴h(x)=ax2﹣3x+1至少要取遍(0,1]中的每一个数,
又h(0)=1,
∴实数a需要满足a≤0或 ![]() ,
,
解得a≤ ![]() .
.
∴实数a的最大值为 ![]() .
.
故选:B.
【考点精析】本题主要考查了函数的值的相关知识点,需要掌握函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市
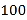 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以 ,
, ,
, ,
, ,
, ,
, ,
, 分组的频率分布直方图如图.
分组的频率分布直方图如图.
(1)求直方图中
 的值;
的值;(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为
 ,
, ,
, ,
, 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取 户居民,则月平均用电量在
户居民,则月平均用电量在 的用户中应抽取多少户?
的用户中应抽取多少户? -
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的内角A,B,C的对边分别为a、b、c,a=btanA,且B为钝角.
(1)证明:B﹣A= ;
;
(2)求sinA+sinC的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=lnx+
 ,m∈R
,m∈R
(1)当m=e(e为自然对数的底数)时,求f(x)的最小值;
(2)讨论函数g(x)=f′(x)﹣ 零点的个数;
零点的个数;
(3)(理科)若对任意b>a>0, <1恒成立,求m的取值范围.
<1恒成立,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 ,
, ,
, 是
是 的动点,过点
的动点,过点 作
作 的垂线,线段
的垂线,线段 的中垂线交
的中垂线交 于点
于点 ,
, 的轨迹为
的轨迹为 .
.(1)求轨迹
 的方程;
的方程;(2)过
 且与坐标轴不垂直的直线交曲线
且与坐标轴不垂直的直线交曲线 于
于 两点,若以线段
两点,若以线段 为直径的圆与直线
为直径的圆与直线 相切,求直线
相切,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题,其中正确命题的个数( )
①若a>|b|,则a2>b2
②若a>b,c>d,则a﹣c>b﹣d
③若a>b,c>d,则ac>bd
④若a>b>o,则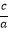 >
>  .
.
A.3个
B.2个
C.1个
D.0个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(1﹣
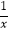 )的定义域为[1,+∞),则函数y=
)的定义域为[1,+∞),则函数y= 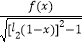 的定义域为 .
的定义域为 .
相关试题

