【题目】设函数f(x)=lnx+ ![]() ,m∈R
,m∈R
(1)当m=e(e为自然对数的底数)时,求f(x)的最小值;
(2)讨论函数g(x)=f′(x)﹣ ![]() 零点的个数;
零点的个数;
(3)(理科)若对任意b>a>0, ![]() <1恒成立,求m的取值范围.
<1恒成立,求m的取值范围.
参考答案:
【答案】
(1)解:当m=e时, ![]() ,x>0,
,x>0,
解f′(x)>0,得x>e,
∴f(x)单调递增;
同理,当0<x<e时,f′(x)<0,f(x)单调递减,
∴f(x)只有极小值f(e),
且f(e)=lne+ ![]() =2,
=2,
∴f(x)的极小值为2
(2)解:∵g(x)= ![]() =
= ![]() =0,
=0,
∴m= ![]() ,
,
令h(x)=x﹣ ![]() ,x>0,m∈R,
,x>0,m∈R,
则h(1)= ![]() ,h′(x)=1﹣x2=(1+x)(1﹣x),
,h′(x)=1﹣x2=(1+x)(1﹣x),
令h′(x)>0,解得0<x<1,
∴h(x)在区间(0,1)上单调递增,值域为(0, ![]() );
);
同理,令h′(x)<0,解得x>1,
∴g(x)要区是(1,+∞)上单调递减,值域为(﹣∞, ![]() ).
).
∴当m≤0,或m= ![]() 时,g(x)只有一个零点;
时,g(x)只有一个零点;
当0<m< ![]() 时,g(x)有2个零点;
时,g(x)有2个零点;
当m> ![]() 时,g(x)没有零点
时,g(x)没有零点
(3)解:(理)对任意b>a>0, ![]() <1恒成立,
<1恒成立,
等价于f(b)﹣b<f(a)﹣a恒成立;
设h(x)=f(x)﹣x=lnx+ ![]() ﹣x(x>0),
﹣x(x>0),
则h(b)<h(a).
∴h(x)在(0,+∞)上单调递减;
∵h′(x)= ![]() ﹣
﹣ ![]() ﹣1≤0在(0,+∞)上恒成立,
﹣1≤0在(0,+∞)上恒成立,
∴m≥﹣x2+x=﹣ ![]() +
+ ![]() (x>0),
(x>0),
∴m≥ ![]() ;
;
对于m= ![]() ,h′(x)=0仅在x=
,h′(x)=0仅在x= ![]() 时成立;
时成立;
∴m的取值范围是[ ![]() ,+∞)
,+∞)
【解析】(1)当m=e时, ![]() ,x>0,由此利用导数性质能求出f(x)的极小值.(2)由g(x)=
,x>0,由此利用导数性质能求出f(x)的极小值.(2)由g(x)= ![]() =
= ![]() =0,得m=
=0,得m= ![]() ,令h(x)=x﹣
,令h(x)=x﹣ ![]() ,x>0,m∈R,则h(1)=
,x>0,m∈R,则h(1)= ![]() ,h′(x)=1﹣x2=(1+x)(1﹣x),由此利用导数性质能求出函数g(x)=f′(x)﹣
,h′(x)=1﹣x2=(1+x)(1﹣x),由此利用导数性质能求出函数g(x)=f′(x)﹣ ![]() 零点的个数.(3)(理)当b>a>0时,f′(x)<1在(0,+∞)上恒成立,由此能求出m的取值范围.
零点的个数.(3)(理)当b>a>0时,f′(x)<1在(0,+∞)上恒成立,由此能求出m的取值范围.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 sin2x﹣
sin2x﹣  cos2x.
cos2x.
(1)求f(x)的最小周期和最小值;
(2)将函数f(x)的图象上每一点的横坐标伸长到原来的两倍,纵坐标不变,得到函数g(x)的图象.当x∈ 时,求g(x)的值域.
时,求g(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市
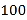 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以 ,
, ,
,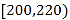 ,
, ,
, ,
, ,
, 分组的频率分布直方图如图.
分组的频率分布直方图如图.
(1)求直方图中
 的值;
的值;(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为
 ,
, ,
, ,
, 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取 户居民,则月平均用电量在
户居民,则月平均用电量在 的用户中应抽取多少户?
的用户中应抽取多少户? -
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的内角A,B,C的对边分别为a、b、c,a=btanA,且B为钝角.
(1)证明:B﹣A= ;
;
(2)求sinA+sinC的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=1﹣
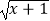 ,g(x)=ln(ax2﹣3x+1),若对任意的x1∈[0,+∞),都存在x2∈R,使得f(x1)=g(x2)成立,则实数a的最大值为( )
,g(x)=ln(ax2﹣3x+1),若对任意的x1∈[0,+∞),都存在x2∈R,使得f(x1)=g(x2)成立,则实数a的最大值为( )
A.2
B.
C.4
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 ,
, ,
, 是
是 的动点,过点
的动点,过点 作
作 的垂线,线段
的垂线,线段 的中垂线交
的中垂线交 于点
于点 ,
, 的轨迹为
的轨迹为 .
.(1)求轨迹
 的方程;
的方程;(2)过
 且与坐标轴不垂直的直线交曲线
且与坐标轴不垂直的直线交曲线 于
于 两点,若以线段
两点,若以线段 为直径的圆与直线
为直径的圆与直线 相切,求直线
相切,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题,其中正确命题的个数( )
①若a>|b|,则a2>b2
②若a>b,c>d,则a﹣c>b﹣d
③若a>b,c>d,则ac>bd
④若a>b>o,则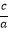 >
>  .
.
A.3个
B.2个
C.1个
D.0个
相关试题

