【题目】如图,点![]() 在以
在以![]() 为直径的圆
为直径的圆![]() 上,
上,![]() 垂直与圆
垂直与圆![]() 所在平面,
所在平面,![]() 为
为![]() 的垂心.
的垂心.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)延长![]() 交
交![]() 于点
于点![]() ,由重心性质及中位线性质可得
,由重心性质及中位线性质可得![]() ,再结合圆的性质得
,再结合圆的性质得![]() ,由已知
,由已知![]() ,可证
,可证![]() 平面
平面![]() ,进一步可得平面
,进一步可得平面![]() 平面
平面![]() (2)以点
(2)以点![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 方向分别为
方向分别为![]() ,
, ![]() ,
, ![]() 轴正方向建立空间直角坐标系,写出各点坐标,利用二面角与二个半平面的法向量的夹角间的关系可求二面角的余弦值.
轴正方向建立空间直角坐标系,写出各点坐标,利用二面角与二个半平面的法向量的夹角间的关系可求二面角的余弦值.
试题解析:(1)如图,延长![]() 交
交![]() 于点
于点![]() .因为
.因为![]() 为
为![]() 的重心,所以
的重心,所以![]() 为
为![]() 的中点.
的中点.
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() .因为
.因为![]() 是圆
是圆![]() 的直径,所以
的直径,所以![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .又
.又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() =
= ![]() ,所以
,所以![]() 平面
平面![]() .即
.即![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以平面
,所以平面![]()
![]() 平面
平面![]() .
.
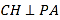
(2)以点![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 方向分别为
方向分别为![]() ,
, ![]() ,
, ![]() 轴正方向建立空间直角坐标系
轴正方向建立空间直角坐标系![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, 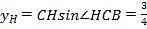 ,
, ![]() ,
, ![]() ,则
,则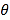 ,
, 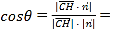 .平面
.平面![]() 即为平面
即为平面![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则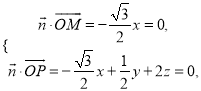 令
令![]() ,得
,得![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,由
,由![]() 平面
平面![]() ,易得
,易得![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,即
,即![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
在![]() 中,由
中,由![]() ,得
,得![]() ,则
,则![]() ,
, ![]() .
.
所以![]() ,
, ![]() .所以
.所以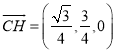 .
.
设二面角![]() 的大小为
的大小为![]() ,则
,则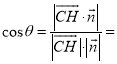
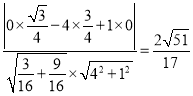 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图给出的是计算
 的值的一个程序框图,判断框内应填入的条件是( )
的值的一个程序框图,判断框内应填入的条件是( ) 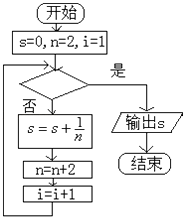
A.i<20
B.i>20
C.i<10
D.i>10 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=1﹣|x|+
 ,若f(x﹣2)>f(3),则x的取值范围是
,若f(x﹣2)>f(3),则x的取值范围是 -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足f(x0)=
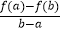 ,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点.若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是 .
,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点.若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,如果执行如图所示的程序框图,输入n=6,m=4,那么输出的p= .
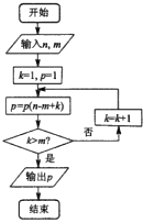
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=cosxsin(x+
 )﹣
)﹣ 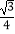 .
.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)△ABC中,角A,B,C所对的边为a,b,c,f( )=
)=  ,B=
,B=  ,a=1,求△ABC的面积.
,a=1,求△ABC的面积.
相关试题

