【题目】定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足f(x0)= ![]() ,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点.若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是 .
,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点.若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是 .
参考答案:
【答案】(0,2)
【解析】解:∵函数f(x)=x2﹣mx﹣1是区间[﹣1,1]上的平均值函数,
∴关于x的方程x2﹣mx﹣1= ![]() 在(﹣1,1)内有实数根.
在(﹣1,1)内有实数根.
即x2﹣mx﹣1=﹣m在(﹣1,1)内有实数根.
即x2﹣mx+m﹣1=0,解得x=m﹣1,x=1.
又1(﹣1,1)
∴x=m﹣1必为均值点,
即﹣1<m﹣1<10<m<2.
∴所求实数m的取值范围是(0,2).
故答案为:(0,2)
函数f(x)=x2﹣mx﹣1是区间[﹣1,1]上的平均值函数,故有x2﹣mx﹣1= ![]() 在(﹣1,1)内有实数根,求出方程的根,让其在(﹣1,1)内,即可求出实数m的取值范围.
在(﹣1,1)内有实数根,求出方程的根,让其在(﹣1,1)内,即可求出实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=1﹣|x|+
 ,若f(x﹣2)>f(3),则x的取值范围是
,若f(x﹣2)>f(3),则x的取值范围是 -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在以
在以 为直径的圆
为直径的圆 上,
上, 垂直与圆
垂直与圆 所在平面,
所在平面, 为
为 的垂心.
的垂心.
(1)求证:平面
 平面
平面 ;
;(2)若
 ,求二面角
,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,如果执行如图所示的程序框图,输入n=6,m=4,那么输出的p= .
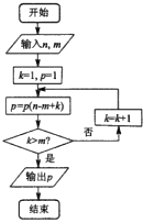
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=cosxsin(x+
 )﹣
)﹣ 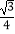 .
.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)△ABC中,角A,B,C所对的边为a,b,c,f( )=
)=  ,B=
,B=  ,a=1,求△ABC的面积.
,a=1,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥P﹣ABCD中,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.

(1)证明:MN∥平面PAD;
(2)若PB与平面ABCD所成的角为45°,求三棱锥C﹣BDN的体积V.
相关试题

