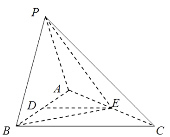
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() .
.
(Ⅰ)求证:![]() (Ⅱ)求二面角
(Ⅱ)求二面角![]() 的大小.
的大小.
参考答案:
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)连接PD,由等腰三角形三线合一,可得PD⊥AB,由DE∥BC,BC⊥AB可得DE⊥AB,进而由线面垂直的判定定理得到AB⊥平面PDE,再由线面垂直的性质得到AB⊥PE;(Ⅱ)以D为原点建立空间直角坐标系,分别求出平面PBE的法向量和平面PAB的法向量,代入向量夹角公式,可得二面角A-PB-E的大小
试题解析:(Ⅰ)连结![]() ,
,![]()
![]() ………
………![]() 分,
分,
∵![]() ,∴
,∴![]() 又
又![]() ,即
,即![]()
∴![]() ,又
,又![]() ,∴
,∴![]() ,
,![]()
∴![]() ………
………![]() 分
分
(Ⅱ)![]() ,
,![]() ,
,![]()
∴![]() ,………
,………![]() 分
分
如图,以D为原点建立空间直角坐标系,
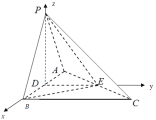
![]() ∴
∴![]()
![]()
![]()
![]() .
.
设平面PBE的法向量![]() ,
,![]()
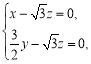 ,令
,令![]() 得
得![]() .………
.………![]() 分[来
分[来
DE⊥平面PAB,![]() 平面PAB的法向量为
平面PAB的法向量为![]() .………
.………![]() 分
分
设二面角的A-PB-E大小为![]() ,由图知,
,由图知,![]() ,
,![]() ,
,
二面角的A-PB-E的大小为![]() .……12分
.……12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 (
( ).
).(1)证明:直线
 过定点;
过定点;(2)若直线不经过第四象限,求
 的取值范围;
的取值范围;(3)若直线
 轴负半轴于
轴负半轴于 ,交
,交 轴正半轴于
轴正半轴于 ,△
,△ 的面积为
的面积为 (
( 为坐标原点),求
为坐标原点),求 的最小值,并求此时直线
的最小值,并求此时直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )

①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行
A.0 B.1 C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
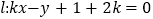 (
(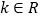 ).
).(1)证明:直线
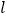 过定点;
过定点;(2)若直线不经过第四象限,求
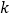 的取值范围;
的取值范围;(3)若直线
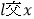 轴负半轴于
轴负半轴于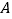 ,交
,交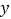 轴正半轴于
轴正半轴于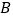 ,△
,△ 的面积为
的面积为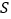 (
(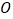 为坐标原点),求
为坐标原点),求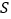 的最小值,并求此时直线
的最小值,并求此时直线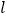 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形
 中,
中,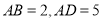 ,
,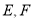 分别在
分别在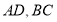 上,且
上,且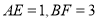 ,沿
,沿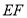 将四边形
将四边形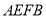 折成四边形
折成四边形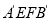 ,使点
,使点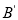 在平面
在平面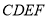 上的射影
上的射影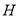 在直线
在直线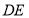 上,且
上,且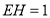 .
.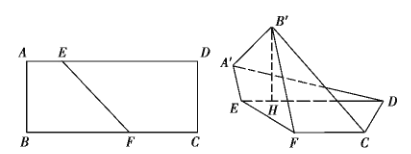
(1)求证:
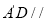 平面
平面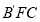 ;
;(2)求
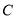 到平面
到平面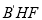 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 (
( ),焦点
),焦点 到准线的距离为
到准线的距离为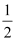 ,过点
,过点
 作直线
作直线 交抛物线
交抛物线 于点
于点 (点
(点 在第一象限).
在第一象限).(Ⅰ)若点
 焦点
焦点 重合,且弦长
重合,且弦长 ,求直线
,求直线 的方程;
的方程; (Ⅱ)若点
 关于
关于 轴的对称点为
轴的对称点为 ,直线
,直线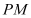 交x轴于点
交x轴于点 ,且
,且 ,求证:点B的坐标是
,求证:点B的坐标是 ,并求点
,并求点 到直线
到直线 的距离
的距离 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,点
的焦点重合,点 在
在 上
上(Ⅰ)求
 的方程;
的方程; (Ⅱ)直线
 不过原点O且不平行于坐标轴,
不过原点O且不平行于坐标轴, 与
与 有两个交点
有两个交点 ,线段
,线段 的中点为
的中点为 ,证明:
,证明: 的斜率与直线
的斜率与直线 的斜率的乘积为定值.
的斜率的乘积为定值.
相关试题

