【题目】已知抛物线![]() (
(![]() ),焦点
),焦点![]() 到准线的距离为
到准线的距离为![]() ,过点
,过点![]()
![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于点
于点![]() (点
(点![]() 在第一象限).
在第一象限).
(Ⅰ)若点![]() 焦点
焦点![]() 重合,且弦长
重合,且弦长![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)若点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 交x轴于点
交x轴于点![]() ,且
,且![]() ,求证:点B的坐标是
,求证:点B的坐标是![]() ,并求点
,并求点![]() 到直线
到直线![]() 的距离
的距离![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ) ![]() 或
或![]() .(Ⅱ)
.(Ⅱ) 
【解析】
试题分析:(Ⅰ)确定抛物线的方程,设出直线方程与抛物线方程联立,利用弦长|PQ|=2,即可求直线l的方程;(Ⅱ)设出直线方程与抛物线方程联立,利用韦达定理,结合向量知识,证明B(-![]() ,0),确定出
,0),确定出![]() ,或m的范围,表示出点B到直线l的距离d,即可求得取值范围
,或m的范围,表示出点B到直线l的距离d,即可求得取值范围
试题解析:(Ⅰ)解:由题意可知,![]() ,故抛物线方程为
,故抛物线方程为![]() ,焦点
,焦点![]() .
.
设直线l的方程为![]() ,
,![]()
![]() ,
,![]() .
.
由 消去x,得
消去x,得![]() .所以△=n2+1>0,
.所以△=n2+1>0,![]() .
.
因为![]() ,点A与焦点F重合,
,点A与焦点F重合,
所以![]() .
.
所以n2=1,即n=±1.所以直线l的方程为![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
(Ⅱ)证明:设直线l的方程为![]() (m≠0),
(m≠0),![]() ,
,![]() 则
则![]()
由 消去x,得
消去x,得![]() ,
,
因为![]() ,所以△=m2+4x0>0,y1+y2=m,y1y2=-x0.
,所以△=m2+4x0>0,y1+y2=m,y1y2=-x0.
设B(xB,0),则![]() .
.
由题意知,![]() ,所以
,所以![]() ,
,
即![]() .
.
显然![]() ,所以
,所以![]() ,即证B(-x0,0).
,即证B(-x0,0).
由题意知,△MBQ为等腰直角三角形,所以![]() ,即
,即![]() ,也即
,也即![]() ,
,
所以![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]() >0,即
>0,即![]()
又因为![]() ,所以
,所以![]() .
. ,
,
所以d的取值范围是 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
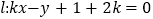 (
(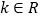 ).
).(1)证明:直线
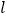 过定点;
过定点;(2)若直线不经过第四象限,求
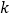 的取值范围;
的取值范围;(3)若直线
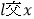 轴负半轴于
轴负半轴于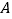 ,交
,交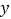 轴正半轴于
轴正半轴于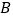 ,△
,△ 的面积为
的面积为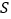 (
(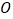 为坐标原点),求
为坐标原点),求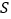 的最小值,并求此时直线
的最小值,并求此时直线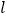 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
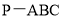 中,
中,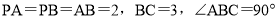 ,
,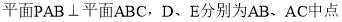 .
.(Ⅰ)求证:
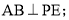 (Ⅱ)求二面角
(Ⅱ)求二面角 的大小.
的大小.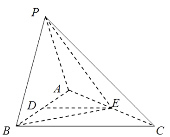
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形
 中,
中, ,
, 分别在
分别在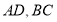 上,且
上,且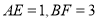 ,沿
,沿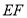 将四边形
将四边形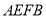 折成四边形
折成四边形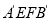 ,使点
,使点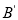 在平面
在平面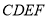 上的射影
上的射影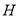 在直线
在直线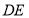 上,且
上,且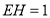 .
.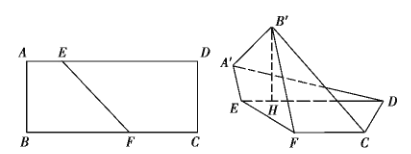
(1)求证:
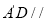 平面
平面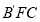 ;
;(2)求
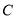 到平面
到平面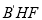 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,点
的焦点重合,点 在
在 上
上(Ⅰ)求
 的方程;
的方程; (Ⅱ)直线
 不过原点O且不平行于坐标轴,
不过原点O且不平行于坐标轴, 与
与 有两个交点
有两个交点 ,线段
,线段 的中点为
的中点为 ,证明:
,证明: 的斜率与直线
的斜率与直线 的斜率的乘积为定值.
的斜率的乘积为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
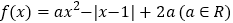 .
.(1)当
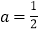 时,解不等式
时,解不等式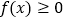 ;
;(2)若
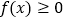 恒成立,求
恒成立,求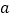 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
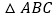 中,边
中,边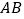 ,
,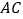 所在直线的方程分别为
所在直线的方程分别为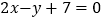 ,
, ,已知
,已知 是
是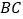 边上一点.
边上一点.(1)若
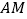 为
为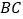 边上的高,求直线
边上的高,求直线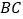 的方程;
的方程;(2)若
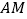 为
为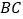 边的中线,求
边的中线,求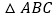 的面积.
的面积.
相关试题

