【题目】已知矩形![]() 中,
中,![]() ,
,![]() 分别在
分别在![]() 上,且
上,且![]() ,沿
,沿![]() 将四边形
将四边形![]() 折成四边形
折成四边形![]() ,使点
,使点![]() 在平面
在平面![]() 上的射影
上的射影![]() 在直线
在直线![]() 上,且
上,且![]() .
.
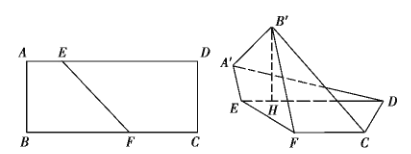
(1)求证:![]() 平面
平面![]() ;
;
(2)求![]() 到平面
到平面![]() 的距离.
的距离.
参考答案:
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(1)证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而当线线平行比较难找时,可以先证面面平行,再转化为线面平行:本题有两组相交直线互相平行,![]() 及
及![]() ,先得线面平行,
,先得线面平行,![]() 平面
平面![]() 及
及![]() 平面
平面![]() ,再得面面平行,平面
,再得面面平行,平面![]()
![]() 平面
平面![]() ,最后得线面平行
,最后得线面平行![]() 平面
平面![]() (2)求点到直线距离,一般利用等体积法,即利用高求对应点到面的距离:因为
(2)求点到直线距离,一般利用等体积法,即利用高求对应点到面的距离:因为![]() ,所以
,所以
试题解析:(1)证明:∵![]() ,∴
,∴![]() ,又
,又![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
∴![]() 平面
平面![]()
同理又![]() ,
,![]() 平面
平面![]()
且![]() ,∴平面
,∴平面![]()
![]() 平面
平面![]()
又![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]()
(2)由题可知,![]() ,
,![]() ,∵
,∵![]() 底面
底面![]() ,∴
,∴![]()
又![]() ,∴
,∴![]() ,
,![]()
![]() ,
,![]()
![]() ,∴
,∴![]()
∴ .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )

①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行
A.0 B.1 C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
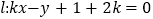 (
(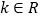 ).
).(1)证明:直线
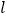 过定点;
过定点;(2)若直线不经过第四象限,求
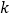 的取值范围;
的取值范围;(3)若直线
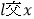 轴负半轴于
轴负半轴于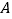 ,交
,交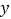 轴正半轴于
轴正半轴于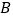 ,△
,△ 的面积为
的面积为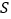 (
(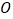 为坐标原点),求
为坐标原点),求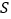 的最小值,并求此时直线
的最小值,并求此时直线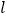 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
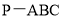 中,
中,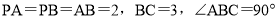 ,
,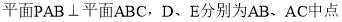 .
.(Ⅰ)求证:
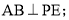 (Ⅱ)求二面角
(Ⅱ)求二面角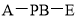 的大小.
的大小.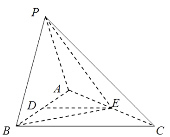
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 (
( ),焦点
),焦点 到准线的距离为
到准线的距离为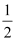 ,过点
,过点
 作直线
作直线 交抛物线
交抛物线 于点
于点 (点
(点 在第一象限).
在第一象限).(Ⅰ)若点
 焦点
焦点 重合,且弦长
重合,且弦长 ,求直线
,求直线 的方程;
的方程; (Ⅱ)若点
 关于
关于 轴的对称点为
轴的对称点为 ,直线
,直线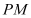 交x轴于点
交x轴于点 ,且
,且 ,求证:点B的坐标是
,求证:点B的坐标是 ,并求点
,并求点 到直线
到直线 的距离
的距离 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,点
的焦点重合,点 在
在 上
上(Ⅰ)求
 的方程;
的方程; (Ⅱ)直线
 不过原点O且不平行于坐标轴,
不过原点O且不平行于坐标轴, 与
与 有两个交点
有两个交点 ,线段
,线段 的中点为
的中点为 ,证明:
,证明: 的斜率与直线
的斜率与直线 的斜率的乘积为定值.
的斜率的乘积为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
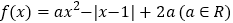 .
.(1)当
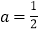 时,解不等式
时,解不等式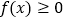 ;
;(2)若
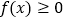 恒成立,求
恒成立,求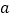 的取值范围.
的取值范围.
相关试题

