【题目】已知直线![]() (
(![]() ).
).
(1)证明:直线![]() 过定点;
过定点;
(2)若直线不经过第四象限,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 轴负半轴于
轴负半轴于![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() ,△
,△![]() 的面积为
的面积为![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的最小值,并求此时直线
的最小值,并求此时直线![]() 的方程.
的方程.
参考答案:
【答案】(1)无论k取何值,直线过定点(-2,1);(2)![]() ;(3)△AOB的面积的最小值为4,此时直线l的方程为
;(3)△AOB的面积的最小值为4,此时直线l的方程为![]() x-y+1+1=0.
x-y+1+1=0.
【解析】【试题分析】(1)将直线方程变形为含参数![]() 的项与 不含参数
的项与 不含参数![]() 的项,借助条件
的项,借助条件![]() 建立方程组,即可求出定点坐标;(2)借助(1)的结论,并数形结合建立关于
建立方程组,即可求出定点坐标;(2)借助(1)的结论,并数形结合建立关于![]() 的不等式组求解;(3)先求出两点
的不等式组求解;(3)先求出两点![]() 的坐标,再建立△
的坐标,再建立△![]() 的面积
的面积![]() 关于斜率
关于斜率![]() 的函数,运用基本不等式求最小值,并借助函数取得最小值时的条件求出直线的方程:
的函数,运用基本不等式求最小值,并借助函数取得最小值时的条件求出直线的方程:
(1)证明:由已知得: k(x+2)+(1-y)=0,
令 x+2=0 且 1-y=0,得: x=-2, y=1
∴无论k取何值,直线过定点(-2,1)
(2)直线方程可化为![]() ,
,
当![]() 时,要使直线不经过第四象限,则
时,要使直线不经过第四象限,则![]() ,解得
,解得![]() ;
;
当![]() 时,直线为
时,直线为![]() ,符合题意.
,符合题意.
综上:![]() 的取值范围是
的取值范围是![]() 。
。
(3)令y=0得:A点坐标为![]() ,令x=0得:B点坐标为(0,2k+1)(k>0),
,令x=0得:B点坐标为(0,2k+1)(k>0),
∴S△AOB=![]()
![]() |2k+1|=
|2k+1|=![]() (2k+1)=
(2k+1)=![]() ≥
≥![]() (4+4)=4
(4+4)=4
当且仅当4k=![]() ,即k=
,即k=![]() 时取等号.
时取等号.
即△AOB的面积的最小值为4,此时直线l的方程为![]() x-y+1+1=0,
x-y+1+1=0,
即 x-2y+4=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
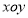 中,已知点
中,已知点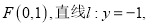
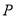 为平面上的动点,且过点
为平面上的动点,且过点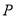 作
作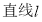 的垂线,垂足为
的垂线,垂足为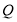 ,满足:
,满足: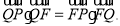
(Ⅰ)求动点
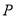 的轨迹
的轨迹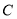 的方程;
的方程;(Ⅱ)在轨迹
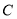 上求一点
上求一点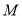 ,使得
,使得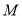 到直线
到直线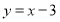 的距离最短,并求出最短距离.
的距离最短,并求出最短距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )

①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行
A.0 B.1 C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 其中
其中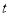 是实数.设
是实数.设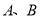 为该函数图像上的两点,横坐标分别为
为该函数图像上的两点,横坐标分别为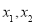 ,且
,且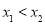 .
.(1求
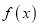 的单调区间和极值;
的单调区间和极值;(2)若
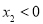 ,函数
,函数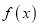 的图像在点
的图像在点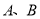 处的切线互相垂直,求
处的切线互相垂直,求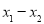 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )

①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行
A.0 B.1 C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
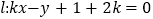 (
(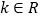 ).
).(1)证明:直线
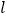 过定点;
过定点;(2)若直线不经过第四象限,求
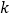 的取值范围;
的取值范围;(3)若直线
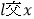 轴负半轴于
轴负半轴于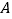 ,交
,交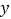 轴正半轴于
轴正半轴于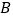 ,△
,△ 的面积为
的面积为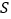 (
(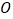 为坐标原点),求
为坐标原点),求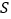 的最小值,并求此时直线
的最小值,并求此时直线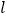 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
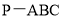 中,
中,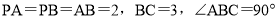 ,
,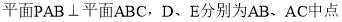 .
.(Ⅰ)求证:
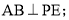 (Ⅱ)求二面角
(Ⅱ)求二面角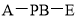 的大小.
的大小.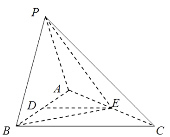
相关试题

