【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为直角梯形,
为直角梯形,![]() 平面
平面 ![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() .
.

(1)求证:![]() 平面
平面 ![]() ;
;
(2)设![]() ,求点
,求点![]() 到平面
到平面 ![]() 的距离.
的距离.
参考答案:
【答案】(1)见解析,(2)![]()
【解析】
试题分析:(1)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(2)利用棱锥的体积公式![]() 求体积.(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.(4)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.
求体积.(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.(4)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.
试题解析:(1)证明:
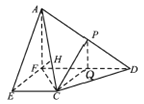
(方法一)设线段![]() 的中点为
的中点为![]() ,连接
,连接![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]()
∵![]() ,且
,且![]() ,∴四边形
,∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() .
.
又![]() ,∴平面
,∴平面 ![]() 平面
平面![]() .
.
∵![]() 平面
平面 ![]() ,∴
,∴![]() 平面
平面 ![]() .
.
(方法二)设线段![]() 的中点为
的中点为![]() ,连接
,连接![]() .
.
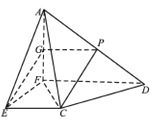
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,且
,且![]() .
.
又∵![]() ,且
,且![]() ,∴
,∴![]() ,∴四边形
,∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() .
.
∵![]() 平面
平面 ![]() 平面
平面 ![]() ,
,
∴![]() 平面
平面 ![]()
(2)解:(方法一)∵四边形![]() 为直角梯形,
为直角梯形,![]() .
.
∴四边形![]() 为正方形,
为正方形,![]() 为等腰直角三角形.
为等腰直角三角形.
∴![]() ,即
,即![]() .
.
又∵![]() 平面
平面 ![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() 平面
平面 ![]() ,面
,面![]() 平面
平面 ![]() ,
,
∴平面 ![]() 平面
平面 ![]()
过![]() 作
作![]() 于点
于点![]() ,则
,则![]() 平面
平面 ![]() ,即
,即![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,点
,点![]() 到平面
到平面 ![]() 的距离为
的距离为![]()
(方法二)设点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
由方法一得,![]() 平面
平面 ![]() ,∴
,∴![]() ,
,
∴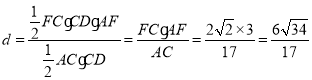 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在12件同类型的零件中有2件次品,抽取3次进行检验,每次抽取1件,并且取出后不再放回,若以ξ和η分别表示取到的次品数和正品数.
(1)求ξ的分布列、均值和方差;
(2)求η的分布列、均值和方差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4),现从袋中任取一球,X表示所取球的标号.
(1)求X的分布列,均值和方差;
(2)若Y=aX+b,E(Y)=1,D(Y)=11,试求a,b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
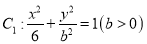 的左、右焦点分别为
的左、右焦点分别为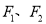 ,点
,点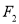 也为抛物线
也为抛物线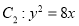 的焦点,过点
的焦点,过点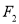 的直线
的直线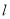 交抛物线
交抛物线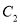 于
于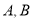 两点.
两点.(Ⅰ)若点
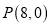 满足
满足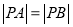 ,求直线
,求直线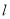 的方程;
的方程;(Ⅱ)
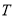 为直线
为直线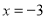 上任意一点,过点
上任意一点,过点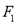 作
作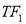 的垂线交椭圆
的垂线交椭圆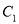 于
于 两点,求
两点,求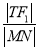 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若方程
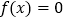 有两个小于2的不等实根,求实数a的取值范围;
有两个小于2的不等实根,求实数a的取值范围;(2)若不等式
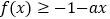 对任意
对任意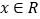 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;(3)若函数
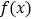 在[0,2]上的最大值为4,求实数a的值.
在[0,2]上的最大值为4,求实数a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间,上课开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,并趋于稳定.分析结果和实验表明,设提出和讲述概念的时间为
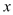 (单位:分),学生的接受能力为
(单位:分),学生的接受能力为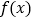 (
(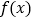 值越大,表示接受能力越强),
值越大,表示接受能力越强),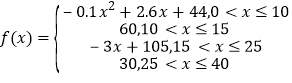
(1)开讲后多少分钟,学生的接受能力最强?能维持多少时间?
(2)试比较开讲后5分钟、20分钟、35分钟,学生的接受能力的大小;(3)若一个数学难题,需要56的接受能力以及12分钟时间,老师能否及时在学生一直达到所需接受能力的状态下讲述完这个难题?
-
科目: 来源: 题型:
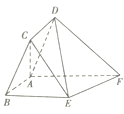
查看答案和解析>>【题目】如图,在平行四边形
 中,
中,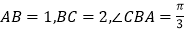 ,四边形
,四边形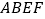 为直角梯形,
为直角梯形,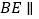 ∥
∥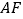 ,
,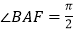 ,
,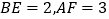 , 平面
, 平面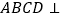 平面
平面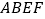 .
.
(1)求证:
 ;
;(2)求平面
 与平面
与平面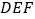 所成锐二面角的余弦值.
所成锐二面角的余弦值.
相关试题

