【题目】如图,在平行四边形![]() 中,
中,![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() , 平面
, 平面![]() 平面
平面![]() .
.
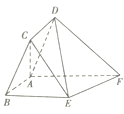
(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】【试题分析】(1)依据题设条件及勾股定理先证线![]() 垂直,借助题设条件,运用
垂直,借助题设条件,运用![]() 性质定理进行推证;(2)建立空间直角坐标系,借助向量的坐标形式的运算及数量积公式求出两平面所成锐角二面角的余弦值:
性质定理进行推证;(2)建立空间直角坐标系,借助向量的坐标形式的运算及数量积公式求出两平面所成锐角二面角的余弦值:
(1)在△ABC中,![]() 所以
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又因为平面ABCD⊥平面ABEF,平面ABCD![]() 平面ABEF=AB,AC
平面ABEF=AB,AC![]() 平面ABCD,所以
平面ABCD,所以![]() 平面ABEF..
平面ABEF..
(2) 如图建立空间直角坐标系,则A(0,0,0),B(1,0,0),![]() ,D(
,D(![]() ,E(1,2,0),F(0,3,0),
,E(1,2,0),F(0,3,0),![]() 是平面ABCD的一个法向量.
是平面ABCD的一个法向量.
设平面DEF的法向量为![]() ,又
,又![]() ,
,![]() ,
,
![]() ,则
,则![]() ,得
,得 ,取
,取![]() 则
则![]() 。
。
故![]() 是平面DEF的一个法向量.设平面ABCD与平面DEF所成的锐二面角为
是平面DEF的一个法向量.设平面ABCD与平面DEF所成的锐二面角为![]() ,则
,则![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,四边形
中,四边形 为直角梯形,
为直角梯形,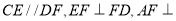 平面
平面  ,
, 为
为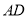 的中点,
的中点, .
.
(1)求证:
 平面
平面  ;
;(2)设
 ,求点
,求点 到平面
到平面  的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若方程
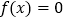 有两个小于2的不等实根,求实数a的取值范围;
有两个小于2的不等实根,求实数a的取值范围;(2)若不等式
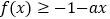 对任意
对任意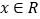 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;(3)若函数
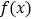 在[0,2]上的最大值为4,求实数a的值.
在[0,2]上的最大值为4,求实数a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间,上课开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,并趋于稳定.分析结果和实验表明,设提出和讲述概念的时间为
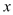 (单位:分),学生的接受能力为
(单位:分),学生的接受能力为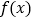 (
(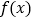 值越大,表示接受能力越强),
值越大,表示接受能力越强),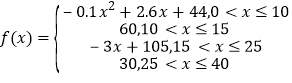
(1)开讲后多少分钟,学生的接受能力最强?能维持多少时间?
(2)试比较开讲后5分钟、20分钟、35分钟,学生的接受能力的大小;(3)若一个数学难题,需要56的接受能力以及12分钟时间,老师能否及时在学生一直达到所需接受能力的状态下讲述完这个难题?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
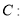
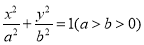 过点
过点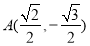 ,离心率为
,离心率为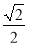 ,
,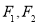 分别为左右焦点.
分别为左右焦点.(1)求椭圆
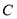 的标准方程;
的标准方程;(2)若
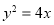 上存在两个点
上存在两个点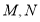 ,椭圆上有两个点
,椭圆上有两个点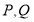 满足
满足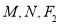 三点共线,
三点共线,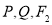 三点共线,且
三点共线,且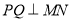 ,求四边形
,求四边形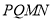 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在2016年6月英国“脱欧”公投前夕,为了统计该国公民是否有“留欧”意愿,该国某中学数学兴趣小组随机抽查了50名不同年龄层次的公民,调查统计他们是赞成“留欧”还是反对“留欧”.现已得知50人中赞成“留欧”的占60%,统计情况如下表:
年龄层次
赞成“留欧”
反对“留欧”
合计
18岁—19岁
6
50岁及50岁以上
10
合计
50
(1)请补充完整上述列联表;
(2)请问是否有97.5%的把握认为赞成“留欧”与年龄层次有关?请说明理由.
参考公式与数据:
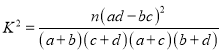 ,其中
,其中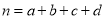
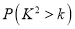
0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
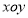 中,已知点
中,已知点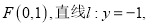
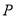 为平面上的动点,且过点
为平面上的动点,且过点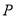 作
作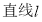 的垂线,垂足为
的垂线,垂足为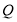 ,满足:
,满足: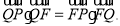
(Ⅰ)求动点
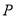 的轨迹
的轨迹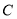 的方程;
的方程;(Ⅱ)在轨迹
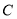 上求一点
上求一点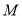 ,使得
,使得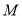 到直线
到直线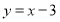 的距离最短,并求出最短距离.
的距离最短,并求出最短距离.
相关试题

