【题目】如图,四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点. 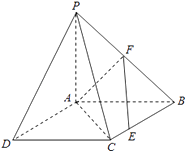
(1)求证:AF⊥EF;
(2)求二面角A﹣PC﹣B的平面角的正弦值.
参考答案:
【答案】
(1)证明:∵四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,
∴PA⊥AD,PA⊥AB,又AD∩AB=A,AB⊥BC,
∴PA⊥平面ABCD,又BC面ABCD,∴PA⊥BC,
∵AB∩PA=A,∴BC⊥面PAB,
∴BC⊥AF,
∵△PAB是以A为直角顶点的等腰直角三角形,F是PB中点,
∴AF⊥PB,
又PB∩BC=B,∴AF⊥平面PBC,
∵EF平面PBC,∴AF⊥EF
(2)解:以A为原点,AD为x轴,AB为y轴,P为z轴,
建立空间直角坐标系,

设AB=1,则A(0,0,0),B(0,1,0),C(1,1,0),P(0,0,1),
![]() =(0,0,1),
=(0,0,1), ![]() =(1,1,0),
=(1,1,0),
设平面APC的法向量 ![]() =(x,y,z),
=(x,y,z),
则  ,取x=1,得
,取x=1,得 ![]() =(1,﹣1,0),
=(1,﹣1,0),
![]() =(0,1,﹣1),
=(0,1,﹣1), ![]() =(1,1,﹣1),
=(1,1,﹣1),
设平面PBC的法向量 ![]() =(a,b,c),
=(a,b,c),
则  ,取b=1,得
,取b=1,得 ![]() =(0,1,1),
=(0,1,1),
|cos< ![]() >|=|
>|=| ![]() |=
|= ![]() ,
,
∴< ![]() >=60°,又sin60°=
>=60°,又sin60°= ![]() ,
,
∴二面角A﹣PC﹣B的平面角的正弦值为 ![]() .
.
【解析】(1)由已知得PA⊥AD,PA⊥AB,AB⊥BC,从而PA⊥BC,进而BC⊥面PAB,又AF⊥PB,由此能证明AF⊥EF.(2)以A为原点,AD为x轴,AB为y轴,P为z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣PC﹣B的平面角的正弦值.
【考点精析】关于本题考查的空间中直线与直线之间的位置关系,需要了解相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=(log2x)2﹣2alog2x+b(x>0).当x=
 时,f(x)有最小值﹣1.
时,f(x)有最小值﹣1.
(1)求a与b的值;
(2)求满足f(x)<0的x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,D是BC的中点.
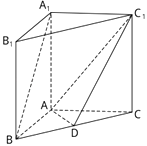
(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求几何体ABD﹣A1B1C1的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数f(x)=ax2+bx+c(a,b,c∈R)满足f(x+1)﹣f(x)=4x+1,且f(0)=3.
(1)求f(x)的解析式;
(2)设g(x)=f(2x),求g(x)在[﹣3,0]的最大值与最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意实数a,b,c,d,以下四个命题中的真命题是( )
A.若a>b,c≠0则ac>bc
B.若a>b>o,c>d则ac>bd
C.若a>b,则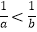
D.若ac2>bc2则a>b -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 (
( )离心率为
)离心率为 ,过点
,过点 的椭圆的两条切线相互垂直.
的椭圆的两条切线相互垂直.(1)求此椭圆的方程;
(2)若存在过点
 的直线
的直线 交椭圆于
交椭圆于 两点,使得
两点,使得 (
( 为右焦点),求
为右焦点),求 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  是
是 的导函数.
的导函数.(1)若
 在
在 处的切线方程为
处的切线方程为 ,求
,求 的值;
的值;(2)若
 且
且 在
在 时取得最小值,求
时取得最小值,求 的取值范围;
的取值范围;(3)在(1)的条件下,当
 时,
时,  .
.
相关试题

