搜索
【题目】已知椭圆
（
）离心率为
，过点
的椭圆的两条切线相互垂直.
（1）求此椭圆的方程；
（2）若存在过点
的直线
交椭圆于
两点，使得
（
为右焦点），求
的范围.
参考答案：
【答案】（1）
；（2）
或
.
【解析】试题分析：（1）根据椭圆的对称性可知，两条切线斜率为
，由此求得切线的方程，联立切线的方程和椭圆的方程，利用判别式等于零列一个方程，结合离心率为
可求得
的值.（2）设出直线
的方程，联立直线的方程和椭圆的方程，消去
，写出韦达定理，将坐标代入
可求得直线方程两个参数的等量关系，由此求得
的取值范围.
试题解析：
（1）由椭圆的对称性，不妨设在
轴上方的切点为
， 
轴下方的切点为
，则
， 
的直线方程为
，
所以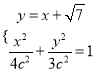
， 
，则
，所以方程为椭圆方程为
。
（2）令
的方程为
， 
，则
，
， 
， 
，
=
所以
有解，
所以
，则
或
-
科目： 来源： 题型：
查看答案和解析>>【题目】若二次函数f（x）=ax2+bx+c（a，b，c∈R）满足f（x+1）﹣f（x）=4x+1，且f（0）=3．
（1）求f（x）的解析式；
（2）设g（x）=f（2x），求g（x）在[﹣3，0]的最大值与最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD是正方形，△PAB与△PAD均是以A为直角顶点的等腰直角三角形，点F是PB的中点，点E是边BC上的任意一点．
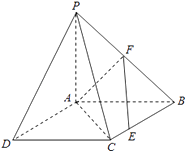
（1）求证：AF⊥EF；
（2）求二面角A﹣PC﹣B的平面角的正弦值． -
科目： 来源： 题型：
查看答案和解析>>【题目】对于任意实数a，b，c，d，以下四个命题中的真命题是（ ）
A.若a＞b，c≠0则ac＞bc
B.若a＞b＞o，c＞d则ac＞bd
C.若a＞b，则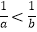
D.若ac2＞bc2则a＞b -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
， 
是
的导函数.（1）若
在
处的切线方程为
，求
的值；（2）若
且
在
时取得最小值，求
的取值范围；（3）在（1）的条件下，当
时， 
. -
科目： 来源： 题型：
查看答案和解析>>【题目】点P是椭圆
上的一点，F1和F2是焦点，且 
，则△F1PF2的周长为 ， △F1PF2的面积为 ． -
科目： 来源： 题型：
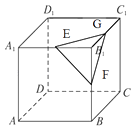
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中，E，F，G分别为A1B1 ， BB1 ， B1C1的中点，则AC1与D1E所成角的余弦值为 ， AC1与平面EFG所成角的正弦值为 ．
相关试题
