搜索
【题目】如图，在直三棱柱ABC﹣A1B1C1中，D是BC的中点．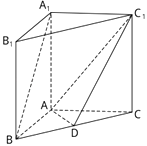 
（1）求证：A1B∥平面ADC1；
（2）若AB⊥AC，AB=AC=1，AA1=2，求几何体ABD﹣A1B1C1的体积．
参考答案：
【答案】
（1）证明：连接A1C，交AC1于点E，
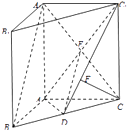
则点E是A1C及AC1的中点．
连接DE，则DE∥A1B．
因为DE平面ADC1，所以A1B∥平面ADC1
（2）解：∵AB⊥AC，AB=AC=1，AA1=2，
∴几何体ABD﹣A1B1C1的体积：
V= 
﹣ 
=S△ABC×AA1﹣ 
= 
﹣ 
=1﹣ 
= 
．
【解析】（1）连接A1C，交AC1于点E，连接DE，则DE∥A1B．由此能证明A1B∥平面ADC1 ． （2）几何体ABD﹣A1B1C1的体积V= ﹣ ，由此能求出结果．
【考点精析】根据题目的已知条件，利用直线与平面平行的判定的相关知识可以得到问题的答案，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设椭圆C：
的离心率e=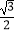 
，左顶点M到直线 
=1的距离d=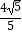 
，O为坐标原点．
（1）求椭圆C的方程；
（2）设直线l与椭圆C相交于A，B两点，若以AB为直径的圆经过坐标原点，证明：点O到直线AB的距离为定值；
（3）在（2）的条件下，试求△AOB的面积S的最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】三棱锥P﹣ABC中，PO⊥面ABC，垂足为O，若PA⊥BC，PC⊥AB，求证：
（1）AO⊥BC
（2）PB⊥AC． -
科目： 来源： 题型：
查看答案和解析>>【题目】设f（x）=（log2x）2﹣2alog2x+b（x＞0）．当x=
时，f（x）有最小值﹣1．
（1）求a与b的值；
（2）求满足f（x）＜0的x的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】若二次函数f（x）=ax2+bx+c（a，b，c∈R）满足f（x+1）﹣f（x）=4x+1，且f（0）=3．
（1）求f（x）的解析式；
（2）设g（x）=f（2x），求g（x）在[﹣3，0]的最大值与最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD是正方形，△PAB与△PAD均是以A为直角顶点的等腰直角三角形，点F是PB的中点，点E是边BC上的任意一点．
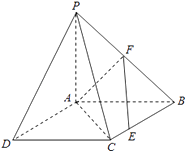
（1）求证：AF⊥EF；
（2）求二面角A﹣PC﹣B的平面角的正弦值． -
科目： 来源： 题型：
查看答案和解析>>【题目】对于任意实数a，b，c，d，以下四个命题中的真命题是（ ）
A.若a＞b，c≠0则ac＞bc
B.若a＞b＞o，c＞d则ac＞bd
C.若a＞b，则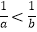
D.若ac2＞bc2则a＞b
相关试题
