【题目】若对任意的![]() ,存在实数
,存在实数![]() ,使
,使![]() 恒成立,则实数
恒成立,则实数![]() 的最大值为__________.
的最大值为__________.
参考答案:
【答案】9
【解析】分析:对任意的x∈[1,5],存在实数a,使![]() 恒成立,
恒成立,![]() .令f(x)=
.令f(x)=![]() +a,x∈[1,4].(b>0).f′(x)=1﹣
+a,x∈[1,4].(b>0).f′(x)=1﹣![]() =
=![]() =
=![]() .对b分类讨论,利用导数研究函数的单调性极值与最值即可得出.
.对b分类讨论,利用导数研究函数的单调性极值与最值即可得出.
详解:对任意的![]() ,存在实数
,存在实数![]() ,使
,使![]() 恒成立,
恒成立,
即![]()
令f(x)=![]() +a,x∈[1,4].(b>0).
+a,x∈[1,4].(b>0).
f′(x)=1﹣![]() =
=![]() =
=![]() .
.
对b分类讨论:
![]() ≥4时,函数f(x)在x∈[1,4]上单调递减:f(1)=1+a+b
≥4时,函数f(x)在x∈[1,4]上单调递减:f(1)=1+a+b![]() ,f(4)=4+
,f(4)=4+![]() +a
+a![]() ,即
,即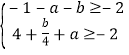 ,解得
,解得![]() ,舍去.
,舍去.
1<![]() <4时,函数f(x)在x∈[1,
<4时,函数f(x)在x∈[1,![]() )上单调递减,在(
)上单调递减,在(![]() ,4]上单调递增.f(
,4]上单调递增.f(![]() )=2
)=2![]() +a=﹣2,f(4)=4+
+a=﹣2,f(4)=4+![]() +a≤2,f(1)=1+a+b≤2,
+a≤2,f(1)=1+a+b≤2,
其中必有一个取等号,解得b=9,a=﹣8.
0<![]() ≤1时,不必要考虑.
≤1时,不必要考虑.
综上可得:b的最大值为9.
故答案为:9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
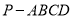 中,四边形
中,四边形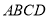 是菱形,
是菱形, 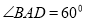 ,又
,又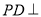 平面
平面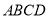 ,
,点
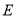 是棱
是棱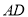 的中点,
的中点, 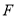 在棱
在棱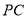 上,且
上,且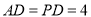 .
.(1)证明:平面
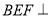 平面
平面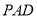 ;
;(2)若
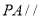 平面
平面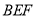 ,求四棱锥
,求四棱锥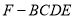 的体积.
的体积.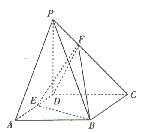
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条光线经过P(2,3)点,射在直线l:x+y+1=0上,反射后穿过点Q(1,1).
(1)求入射光线的方程;
(2)求这条光线从P到Q的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设|θ|<
 ,n为正整数,数列{an}的通项公式an=sin
,n为正整数,数列{an}的通项公式an=sin 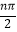 tannθ,其前n项和为Sn
tannθ,其前n项和为Sn
(1)求证:当n为偶函数时,an=0;当n为奇函数时,an=(﹣1)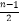 tannθ;
tannθ;
(2)求证:对任何正整数n,S2n= sin2θ[1+(﹣1)n+1tan2nθ].
sin2θ[1+(﹣1)n+1tan2nθ]. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在等腰梯形
 中,
中,  .把
.把 沿
沿 折起,使得
折起,使得 ,得到四棱锥
,得到四棱锥 .如图2所示.
.如图2所示.
(1)求证:面
 面
面 ;
;(2)求平面
 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 为圆
为圆 的圆心,
的圆心,  是圆上动点,点
是圆上动点,点 在圆的半径
在圆的半径 上,且有点
上,且有点 和
和 上的点
上的点 ,满足
,满足
(1)当
 在圆上运动时,求点
在圆上运动时,求点 的轨迹方程;
的轨迹方程;(2)若斜率为
 的直线
的直线 与圆
与圆 相切,与(1)中所求点
相切,与(1)中所求点 的轨迹教育不同的两点
的轨迹教育不同的两点
 是坐标原点,且
是坐标原点,且 时,求
时,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
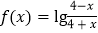 ,其中
,其中 .
.(I)判断并证明函数
 的奇偶性;
的奇偶性;(II)判断并证明函数
 在
在 上的单调性;
上的单调性;(III)是否存在这样的负实数
 ,使
,使 对一切
对一切 恒成立,若存在,试求出
恒成立,若存在,试求出 取值的集合;若不存在,说明理由.
取值的集合;若不存在,说明理由.
相关试题

