【题目】如图1所示,在等腰梯形![]() 中,
中, ![]() .把
.把![]() 沿
沿![]() 折起,使得
折起,使得![]() ,得到四棱锥
,得到四棱锥![]() .如图2所示.
.如图2所示.

(1)求证:面![]() 面
面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
参考答案:
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先由平面几何知识证明![]() ,可得
,可得![]() 面
面![]() ,从而得
,从而得![]() ,进而可得
,进而可得![]() ,于是
,于是![]() 面
面![]() ,最后由面面垂直的判定定理可得结论;(2)以点
,最后由面面垂直的判定定理可得结论;(2)以点![]() 为原点,以
为原点,以![]() 所在直线分别为
所在直线分别为![]() 轴,建立如图所示的空间直角坐标系,分别求出两半平面的一个法向量,根据空间向量夹角余弦公式可得结果.
轴,建立如图所示的空间直角坐标系,分别求出两半平面的一个法向量,根据空间向量夹角余弦公式可得结果.
试题解析:(1)证明:在等腰梯形![]() 中
中![]() ,可知
,可知![]() .因为
.因为![]() ,可得
,可得![]() .
.
又因为![]() ,即
,即![]() ,则
,则![]() .
.
又![]() ,可得
,可得![]() 面
面![]() ,故
,故![]() .
.
又因为![]() ,则
,则![]() ,
,
![]() ,则
,则![]() ,
,
所以![]() ,
,
又![]() ,所以
,所以![]() 面
面![]() ,
,
又![]() 面
面![]() ,所以面
,所以面![]() 面
面![]() ;
;
(2)
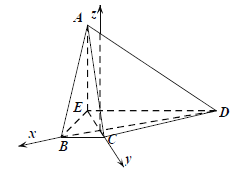
设![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
以点![]() 为原点,以
为原点,以![]() 所在直线分别为
所在直线分别为![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() .
.
在![]() 中,∵
中,∵![]() ,
, ![]() ,
,
∴![]() ,则
,则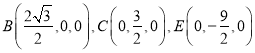 ,
,
∵![]() ,
,
∴![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴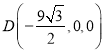 ,
,
∴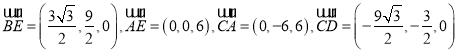 ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由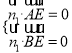 ,得
,得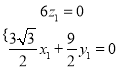 ,
,
取![]() ,可得平面
,可得平面![]() 的法向量为
的法向量为![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由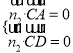 ,得
,得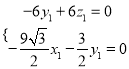 ,
,
取![]() ,可得平面
,可得平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,
,
则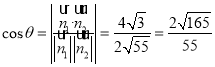 ,
,
所以平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的圆心在直线上
 ,且与直线
,且与直线 相切于点
相切于点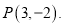
(1)求圆C的方程;
(2)是否存在过点
 的直线
的直线 与圆C交于
与圆C交于 两点,且
两点,且 的面积为
的面积为 (O为坐标原点),若存在,求出直线
(O为坐标原点),若存在,求出直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直三棱柱
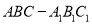 中,
中, 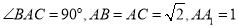 ,点
,点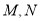 分别为
分别为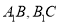 的中点.
的中点.(1)求证:
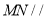 平面
平面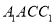 ;
;(2)求三棱锥
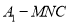 的体积(锥体的体积公式
的体积(锥体的体积公式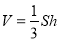 ,其中
,其中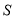 为底面面积,
为底面面积, 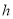 为高)
为高) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
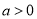 ,且
,且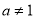 .设
.设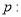 函数
函数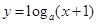 在区间
在区间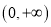 内单调递减;
内单调递减;  曲线
曲线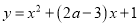 与
与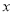 轴交于不同的两点,如果“
轴交于不同的两点,如果“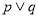 ”为真命题,“
”为真命题,“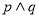 ”为假命题,求实数
”为假命题,求实数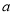 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  的长轴长为6,且椭圆
的长轴长为6,且椭圆 与圆
与圆 :
:  的公共弦长为
的公共弦长为 .
.(1)求椭圆
 的方程.
的方程.(2)过点
 作斜率为
作斜率为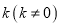 的直线
的直线 与椭圆
与椭圆 交于两点
交于两点 ,
,  ,试判断在
,试判断在 轴上是否存在点
轴上是否存在点 ,使得
,使得 为以
为以 为底边的等腰三角形.若存在,求出点
为底边的等腰三角形.若存在,求出点 的横坐标的取值范围,若不存在,请说明理由.
的横坐标的取值范围,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,某物流公司每天的业务中,从甲地到乙地的可配送的货物量
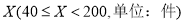 的频率分布直方图,如图所示,将频率视为概率,回答以下问题.
的频率分布直方图,如图所示,将频率视为概率,回答以下问题.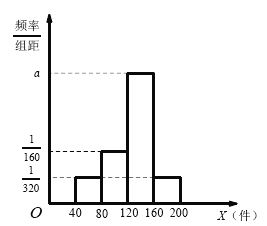
(1)求该物流公司每天从甲地到乙地平均可配送的货物量;
(2)该物流公司拟购置货车专门运营从甲地到乙地的货物,一辆货车每天只能运营一趟,每辆车每
趟最多只能装载40 件货物,满载发车,否则不发车。若发车,则每辆车每趟可获利1000 元;若未发车,
则每辆车每天平均亏损200 元。为使该物流公司此项业务的营业利润最大,该物流公司应该购置几辆货
车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
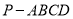 中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,
中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2, 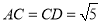 .
.(1)求证:PD⊥平面PAB;
(2)求直线PB与平面PCD所成角的正弦值.
相关试题

