【题目】已知函数![]() ,其中
,其中![]() .
.
(I)判断并证明函数![]() 的奇偶性;
的奇偶性;
(II)判断并证明函数![]() 在
在![]() 上的单调性;
上的单调性;
(III)是否存在这样的负实数![]() ,使
,使![]() 对一切
对一切![]() 恒成立,若存在,试求出
恒成立,若存在,试求出![]() 取值的集合;若不存在,说明理由.
取值的集合;若不存在,说明理由.
参考答案:
【答案】(1)见解析(2)见解析(3)![]()
【解析】分析:(I)根据函数奇偶性的定义进行判断即可.
(II)根据函数单调性 定义进行判断.
(III)根据函数奇偶性和单调性的关系将不等式进行转化,利用参数分离法进行求解即可.
详解:
(I)∵![]() ,
,
∴![]() 是奇函数.
是奇函数.
(II)![]() 在
在![]() 上为减函数.
上为减函数.
证明:任取![]() 且
且![]() ,
,
则![]()
![]()
![]() ,
,
∵![]()
![]() ,
,
∴![]() ,
,
得![]() ,得到
,得到![]() ,
,
∴![]() 在
在![]() 上为减函数;
上为减函数;
(III)∵![]()
![]() ,
,
∵![]() 在
在![]() 上为减函数,
上为减函数,
∴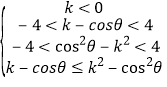 对
对![]() 恒成立
恒成立
由![]() 对
对![]() 恒成立得:
恒成立得:
![]() 对
对![]() 恒成立,
恒成立,
令![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,得
,得![]() ,
,
由![]() 对
对![]() 恒成立得:
恒成立得:
![]() ,由
,由![]() 对
对![]() 恒成立得:
恒成立得:![]() ,
,
即综上所得:![]() ,
,
所以存在这样的![]() ,其范围为
,其范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若对任意的
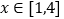 ,存在实数
,存在实数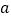 ,使
,使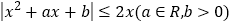 恒成立,则实数
恒成立,则实数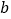 的最大值为__________.
的最大值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在等腰梯形
 中,
中,  .把
.把 沿
沿 折起,使得
折起,使得 ,得到四棱锥
,得到四棱锥 .如图2所示.
.如图2所示.
(1)求证:面
 面
面 ;
;(2)求平面
 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 为圆
为圆 的圆心,
的圆心,  是圆上动点,点
是圆上动点,点 在圆的半径
在圆的半径 上,且有点
上,且有点 和
和 上的点
上的点 ,满足
,满足
(1)当
 在圆上运动时,求点
在圆上运动时,求点 的轨迹方程;
的轨迹方程;(2)若斜率为
 的直线
的直线 与圆
与圆 相切,与(1)中所求点
相切,与(1)中所求点 的轨迹教育不同的两点
的轨迹教育不同的两点
 是坐标原点,且
是坐标原点,且 时,求
时,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC
(1)求三棱锥D-ABC的体积
(2)求证:平面DAC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=
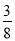 CA,求证:MN∥平面DEF
CA,求证:MN∥平面DEF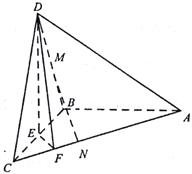
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组.现要从中抽取10名学生,各组内抽取的编号按依次增加10进行系统抽样.
(1)若抽出的一个号码为22,则此号码所在的组数是多少?据此写出所有被抽出学生的号码;
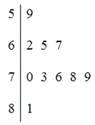
(2)分别统计这10名学生的数学成绩,获得成绩数据的茎叶图如图4所示,求该样本的方差;
(3)在(2)的条件下,从这10名学生中随机抽取两名成绩不低于73分的学生,求被抽取到的两名学生的成绩之和不小于154分的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
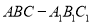 中,底面
中,底面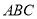 为正三角形,
为正三角形, 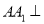 底面
底面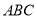 ,且
,且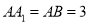 ,
, 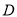 是
是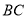 的中点.
的中点.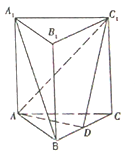
(1)求证:
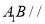 平面
平面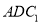 ;
; (2)求证:平面
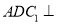 平面
平面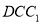 ;
;(3)在侧棱
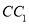 上是否存在一点
上是否存在一点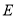 ,使得三棱锥
,使得三棱锥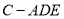 的体积是
的体积是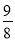 ?若存在,求出
?若存在,求出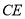 的长;若不存在,说明理由.
的长;若不存在,说明理由.
相关试题

