【题目】已知函数![]() ,在区间
,在区间![]() 内任取两个实数
内任取两个实数![]() ,
,![]() ,且
,且![]() ,若不等式
,若不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
分析:首先,由![]() 的几何意义,得到直线的斜率,然后,得到函数图象上在区间(1,2)内任意两点连线的斜率大于1,从而得到f′(x)=
的几何意义,得到直线的斜率,然后,得到函数图象上在区间(1,2)内任意两点连线的斜率大于1,从而得到f′(x)=![]() >1 在(1,2)内恒成立.分离参数后,转化成 a>2x2+3x+1在(1,2)内恒成立.从而求解得到a的取值范围.
>1 在(1,2)内恒成立.分离参数后,转化成 a>2x2+3x+1在(1,2)内恒成立.从而求解得到a的取值范围.
详解:∵![]() 的几何意义为:
的几何意义为:
表示点(p+1,f(p+1)) 与点(q+1,f(q+1))连线的斜率,
∵实数p,q在区间(0,1)内,故p+1 和q+1在区间(1,2)内.
不等式![]() >1恒成立,
>1恒成立,
∴函数图象上在区间(1,2)内任意两点连线的斜率大于1,
故函数的导数大于1在(1,2)内恒成立.
由函数的定义域知,x>﹣1,
∴f′(x)=![]() >1 在(1,2)内恒成立.
>1 在(1,2)内恒成立.
即 a>2x2+3x+1在(1,2)内恒成立.
由于二次函数y=2x2+3x+1在[1,2]上是单调增函数,
故 x=2时,y=2x2+3x+1在[1,2]上取最大值为15,
∴a≥15
∴a∈[15,+∞).
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
 的极坐标方程是
的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 (
( 为参数).
为参数).(Ⅰ)将曲线
 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;(Ⅱ)若直线
 与曲线
与曲线 相交于
相交于 ,
, 两点,且
两点,且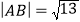 ,求直线
,求直线 的倾斜角
的倾斜角 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】经过市场调查,超市中的某种小商品在过去的近40天的日销售量(单位:件)与价格(单位:元)为时间
 (单位:天)的函数,且日销售量近似满足
(单位:天)的函数,且日销售量近似满足 ,价格近似满足
,价格近似满足 。
。(1)写出该商品的日销售额
 (单位:元)与时间
(单位:元)与时间 (
(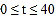 )的函数解析式并用分段函数形式表示该解析式(日销售额=销售量
)的函数解析式并用分段函数形式表示该解析式(日销售额=销售量 商品价格);
商品价格);(2)求该种商品的日销售额
 的最大值和最小值.
的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,将
,将 的图象向右平移两个单位长度,得到函数
的图象向右平移两个单位长度,得到函数 的图象.
的图象.(1)求函数
 的解析式;
的解析式;(2)若方程
 在
在 上有且仅有一个实根,求
上有且仅有一个实根,求 的取值范围;
的取值范围;(3)若函数
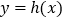 与
与 的图象关于直线
的图象关于直线 对称,设
对称,设 ,已知
,已知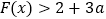 对任意的
对任意的 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=sin(x+
 )的图象上各点的横坐标压缩为原来的
)的图象上各点的横坐标压缩为原来的  倍(纵坐标不变),所得函数在下面哪个区间单调递增( )
倍(纵坐标不变),所得函数在下面哪个区间单调递增( )
A.(﹣ ,
,  )
)
B.(﹣ ,
,  )
)
C.(﹣ ,
,  )
)
D.(﹣ ,
,  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
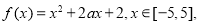
(1)若
 在区间
在区间 上是单调函数,求实数
上是单调函数,求实数 的取值范围.
的取值范围.(2)求函数在
 上的最大值和最小值;
上的最大值和最小值; -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方
 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出 条较为详细的评价信息进行统计,车辆状况的优惠活动评价的
条较为详细的评价信息进行统计,车辆状况的优惠活动评价的 列联表如下:
列联表如下:对优惠活动好评
对优惠活动不满意
合计
对车辆状况好评



对车辆状况不满意



合计



(1)能否在犯错误的概率不超过
 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?(2)为了回馈用户,公司通过
 向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过
向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过 转赠给友.某用户共获得了
转赠给友.某用户共获得了 张骑行券,其中只有
张骑行券,其中只有 张是一元券.现该用户从这
张是一元券.现该用户从这 张骑行券中随机选取
张骑行券中随机选取 张转赠给好友,求选取的
张转赠给好友,求选取的 张中至少有
张中至少有 张是一元券的概率.
张是一元券的概率.参考数据:
















参考公式:
 ,其中
,其中 .
.
相关试题

