【题目】已知函数![]() ,将
,将![]() 的图象向右平移两个单位长度,得到函数
的图象向右平移两个单位长度,得到函数![]() 的图象.
的图象.
(1)求函数![]() 的解析式;
的解析式;
(2)若方程![]() 在
在![]() 上有且仅有一个实根,求
上有且仅有一个实根,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,设
对称,设![]() ,已知
,已知![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
【试题分析】(1)借助平移的知识可直接求得函数解析式;(2)先换元![]() 将问题进行等价转化为
将问题进行等价转化为![]() 有且只有一个根,再构造二次函数
有且只有一个根,再构造二次函数![]() 运用函数方程思想建立不等式组分析求解;(3)先依据题设条件求出函数的解析式
运用函数方程思想建立不等式组分析求解;(3)先依据题设条件求出函数的解析式![]() ,再运用不等式恒成立求出函数
,再运用不等式恒成立求出函数![]() 的最小值:
的最小值:
解:(1) ![]()
(2)设![]() ,则
,则![]() ,原方程可化为
,原方程可化为![]()
于是只须![]() 在
在![]() 上有且仅有一个实根,
上有且仅有一个实根,
法1:设![]() ,对称轴t=
,对称轴t=![]() ,则
,则![]() ① , 或
① , 或 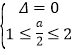 ②
②
由①得 ![]() ,即
,即![]() ,
,![]()
由②得![]() 无解, ,则
无解, ,则![]() 。
。
法2:由![]()
![]() ,得,
,得,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,记
,记![]() ,
,
则![]() 在
在![]() 上是单调函数,因为故要使题设成立,
上是单调函数,因为故要使题设成立,
只须![]() ,即
,即![]() ,
,
从而有![]()
(3)设![]() 的图像上一点
的图像上一点![]() ,点
,点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,
由点![]() 在
在![]() 的图像上,所以
的图像上,所以![]() ,
,
于是![]() 即
即![]() .
.![]() .
.
由![]() ,化简得
,化简得![]() ,设
,设![]() ,即
,即![]() 恒成立.
恒成立.
解法1:设![]() ,对称轴
,对称轴![]()
则![]() ③ 或
③ 或 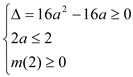 ④
④
由③得![]() , 由④得
, 由④得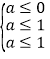 或
或![]() ,即
,即![]() 或
或![]()
综上,![]() .
.
解法2:注意到![]() ,分离参数得
,分离参数得![]() 对任意
对任意![]() 恒成立
恒成立
设![]() ,
,![]() ,即
,即![]()
![]()
可证![]() 在
在![]() 上单调递增
上单调递增 ![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:函数f(x)=x2-2mx+4在[2,+∞)上单调递增,命题q:关于x的不等式mx2+4(m-2)x+4>0的解集为R.若p∨q为真命题,p∧q为假命题,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
 的极坐标方程是
的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 (
( 为参数).
为参数).(Ⅰ)将曲线
 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;(Ⅱ)若直线
 与曲线
与曲线 相交于
相交于 ,
, 两点,且
两点,且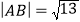 ,求直线
,求直线 的倾斜角
的倾斜角 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】经过市场调查,超市中的某种小商品在过去的近40天的日销售量(单位:件)与价格(单位:元)为时间
 (单位:天)的函数,且日销售量近似满足
(单位:天)的函数,且日销售量近似满足 ,价格近似满足
,价格近似满足 。
。(1)写出该商品的日销售额
 (单位:元)与时间
(单位:元)与时间 (
(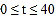 )的函数解析式并用分段函数形式表示该解析式(日销售额=销售量
)的函数解析式并用分段函数形式表示该解析式(日销售额=销售量 商品价格);
商品价格);(2)求该种商品的日销售额
 的最大值和最小值.
的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,在区间
,在区间 内任取两个实数
内任取两个实数 ,
, ,且
,且 ,若不等式
,若不等式 恒成立,则实数
恒成立,则实数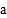 的取值范围是
的取值范围是A.
 B.
B. 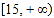 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=sin(x+
 )的图象上各点的横坐标压缩为原来的
)的图象上各点的横坐标压缩为原来的  倍(纵坐标不变),所得函数在下面哪个区间单调递增( )
倍(纵坐标不变),所得函数在下面哪个区间单调递增( )
A.(﹣ ,
,  )
)
B.(﹣ ,
,  )
)
C.(﹣ ,
,  )
)
D.(﹣ ,
,  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
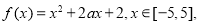
(1)若
 在区间
在区间 上是单调函数,求实数
上是单调函数,求实数 的取值范围.
的取值范围.(2)求函数在
 上的最大值和最小值;
上的最大值和最小值;
相关试题

