【题目】如图,在平面直角坐标系xOy中,过点A(﹣6,0)的直线l1与直线l2:y=2x相交于点B(m,4).
(1)求直线l1的表达式;
(2)过动点P(n,0)且垂于x轴的直线与l1 , l2的交点分别为C,D,当点C位于点D上方时,写出n的取值范围.
参考答案:
【答案】
(1)
解:∵点B在直线l2上,
∴4=2m,
∴m=2,点B(2,4)
设直线l1的表达式为y=kx+b,
由题意 ![]() ,解得
,解得 ![]() ,
,
∴直线l1的表达式为y= ![]() x+3.
x+3.
(2)
解:与图象可知n<2.
【解析】不同考查两条直线平行、相交问题,解题的关键是灵活应用待定系数法,学会利用图象根据条件确定自变量取值范围.
(1)先求出点B坐标,再利用待定系数法即可解决问题;
(2)由图象可知直线l1在直线l2上方即可,由此即可写出n的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
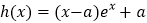 .
.(1)若
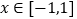 ,求函数
,求函数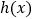 的最小值;
的最小值;(2)当
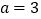 时,若对
时,若对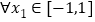 ,
,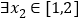 ,使得
,使得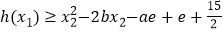 成立,求
成立,求 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根. -
科目: 来源: 题型:
查看答案和解析>>【题目】按照国家环保部发布的新修订的《环境空气质量标准》,规定:PM2.5的年平均浓度不得超过35微克/立方米,国家环保部门在2016年10月1日到2017年1月30日这120天对全国的PM2.5平均浓度的监测数据统计如下:
组别
PM2.5浓度(微克/立方米)
频数(天)
第一组
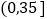
32
第二组
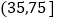
64
第三组
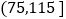
16
第四组
115以上
8
(1)在这120天中抽取30天的数据做进一步分析,每一组应抽取多少天?
(2)在(1)中所抽取的样本PM2.5的平均浓度超过75(微克/立方米)的若干天中,随机抽取2天,求恰好有一天平均浓度超过115(微克/立方米)的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某养殖场需定期购买饲料,已知该场每天需要饲料200千克,每千克饲料的价格为1.8元,饲料的保管费与其他费用平均每千克每天0.03元,购买饲料每次支付运费300元.
(1)求该场多少天购买一次饲料才能使平均每天支付的总费用最少;
(2)若提供饲料的公司规定,当一次购买饲料不少于5吨时,其价格可享受八五折优惠(即原价为85%).问:该场是否应考虑利用此优惠条件?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以直角坐标系的原点
 为极点,
为极点,  轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线
轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线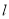 的参数方程为
的参数方程为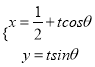 ,(
,( 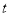 为参数,
为参数, 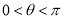 ),曲线
),曲线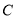 的极坐标方程为
的极坐标方程为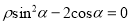 .
.(1)求曲线
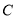 的直角坐标方程;
的直角坐标方程;(2)设直线
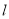 与曲线
与曲线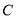 相交于
相交于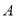 ,
, 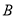 两点,当
两点,当 变化时,求
变化时,求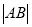 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
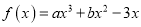 在
在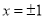 处取得极值.
处取得极值.(1)讨论
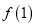 和
和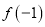 是函数
是函数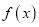 的极大值还是极小值;
的极大值还是极小值;(2)过点
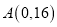 作曲线
作曲线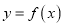 的切线,求此切线方程.
的切线,求此切线方程.
相关试题

