【题目】以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线
轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线![]() 的参数方程为
的参数方程为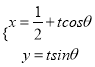 ,(
,( ![]() 为参数,
为参数, ![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)![]() (2)2
(2)2
【解析】试题分析:(1)本问考查极坐标与直角坐标互化公式,根据![]() 可得
可得![]() ,所以曲线C的直角坐标方程为
,所以曲线C的直角坐标方程为![]() ;(2)本问考查直线参数方程标准形式下的几何意义,即将直线参数方程的标准形式
;(2)本问考查直线参数方程标准形式下的几何意义,即将直线参数方程的标准形式 ,代入到曲线C的直角坐标方程,得到关于t的一元二次方程,设
,代入到曲线C的直角坐标方程,得到关于t的一元二次方程,设![]() 两点对应的参数分别为
两点对应的参数分别为![]() ,列出
,列出![]() ,
, ![]() ,
, ![]() ,于是可以求出
,于是可以求出![]() 的最小值.
的最小值.
试题解析:(I)由![]() 由,得
由,得![]()
![]() 曲线
曲线 ![]() 的直角坐标方程为
的直角坐标方程为![]()
(II)将直线![]() 的参数方程代入
的参数方程代入![]() ,得
,得![]()
设![]() 两点对应的参数分别为
两点对应的参数分别为![]() 则
则![]() ,
, ![]() ,
,
![]()
![]()
![]()
当![]() 时,
时, ![]() 的最小值为2.
的最小值为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按照国家环保部发布的新修订的《环境空气质量标准》,规定:PM2.5的年平均浓度不得超过35微克/立方米,国家环保部门在2016年10月1日到2017年1月30日这120天对全国的PM2.5平均浓度的监测数据统计如下:
组别
PM2.5浓度(微克/立方米)
频数(天)
第一组
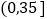
32
第二组
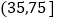
64
第三组
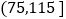
16
第四组
115以上
8
(1)在这120天中抽取30天的数据做进一步分析,每一组应抽取多少天?
(2)在(1)中所抽取的样本PM2.5的平均浓度超过75(微克/立方米)的若干天中,随机抽取2天,求恰好有一天平均浓度超过115(微克/立方米)的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,过点A(﹣6,0)的直线l1与直线l2:y=2x相交于点B(m,4).

(1)求直线l1的表达式;
(2)过动点P(n,0)且垂于x轴的直线与l1 , l2的交点分别为C,D,当点C位于点D上方时,写出n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某养殖场需定期购买饲料,已知该场每天需要饲料200千克,每千克饲料的价格为1.8元,饲料的保管费与其他费用平均每千克每天0.03元,购买饲料每次支付运费300元.
(1)求该场多少天购买一次饲料才能使平均每天支付的总费用最少;
(2)若提供饲料的公司规定,当一次购买饲料不少于5吨时,其价格可享受八五折优惠(即原价为85%).问:该场是否应考虑利用此优惠条件?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
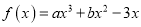 在
在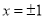 处取得极值.
处取得极值.(1)讨论
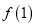 和
和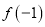 是函数
是函数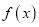 的极大值还是极小值;
的极大值还是极小值;(2)过点
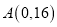 作曲线
作曲线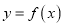 的切线,求此切线方程.
的切线,求此切线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,连接BM,MN,BN.
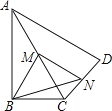
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆
 的左焦点为
的左焦点为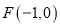 ,过点F做x轴的垂线交椭圆于A,B两点,且
,过点F做x轴的垂线交椭圆于A,B两点,且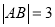 .
.(1)求椭圆C的标准方程:
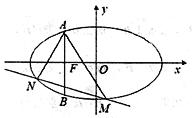
(2)若M,N为椭圆上异于点A的两点,且直线
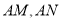 的倾斜角互补,问直线MN的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
的倾斜角互补,问直线MN的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
相关试题

