【题目】已知函数![]() 在
在![]() 处取得极值.
处取得极值.
(1)讨论![]() 和
和![]() 是函数
是函数![]() 的极大值还是极小值;
的极大值还是极小值;
(2)过点![]() 作曲线
作曲线![]() 的切线,求此切线方程.
的切线,求此切线方程.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】第一问由函数![]() 在
在![]() 处取得极值.
处取得极值.
说明了′(1)= ′(-1)=0,得到a,b的值,并代入原式中,判定函数的单调性,得到极值问题。
第二问中,要求过点![]() 作曲线
作曲线![]() 的切线,先设出切点坐标,然后结合导数的几何意义得到斜率,表示切线方程,再将A点代入方程中得到点的坐标,求解得到。
的切线,先设出切点坐标,然后结合导数的几何意义得到斜率,表示切线方程,再将A点代入方程中得到点的坐标,求解得到。
解:(1)′(x)=3ax2+2bx-3,依题意,′(1)= ′(-1)=0,即
3a+2b-3=0,
3a-2b-3=0.解得a=1, b="0."
∴(x)=x3-3x,′(x)=3x2-3=3(x+1)(x-1).
令′(x)=0,得x1=-1,x2=1.
若x∈(-∞,-1)∪(1,+∞),则′(x)>0,故(x)在(-∞,-1),(1,+∞)上是增函数.
若x∈(-1,1),则′(x)<0,故(x)在(-1,1)上是减函数.
所以(-1)=2是极大值,(1)=-2是极小值.
(1)曲线方程为y=x3-3x,点A(0,16)不在曲线上,设切点为M(x0,y0)
则点M的坐标满足y0= x03-3x0,
因为f’(x0)=3(x02-1),故切线方程为
y-y0=3(x02-1)(x-x9)
因为点A在曲线上,则可知16-(x03-3x0)=3(x02-1)(x-x9)
化简得到x0=-2,
所以切点坐标为M(-2,-2),切线方程为9x-y+16=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,过点A(﹣6,0)的直线l1与直线l2:y=2x相交于点B(m,4).

(1)求直线l1的表达式;
(2)过动点P(n,0)且垂于x轴的直线与l1 , l2的交点分别为C,D,当点C位于点D上方时,写出n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某养殖场需定期购买饲料,已知该场每天需要饲料200千克,每千克饲料的价格为1.8元,饲料的保管费与其他费用平均每千克每天0.03元,购买饲料每次支付运费300元.
(1)求该场多少天购买一次饲料才能使平均每天支付的总费用最少;
(2)若提供饲料的公司规定,当一次购买饲料不少于5吨时,其价格可享受八五折优惠(即原价为85%).问:该场是否应考虑利用此优惠条件?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以直角坐标系的原点
 为极点,
为极点,  轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线
轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线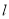 的参数方程为
的参数方程为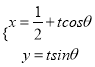 ,(
,( 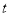 为参数,
为参数, 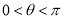 ),曲线
),曲线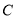 的极坐标方程为
的极坐标方程为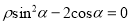 .
.(1)求曲线
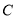 的直角坐标方程;
的直角坐标方程;(2)设直线
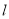 与曲线
与曲线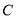 相交于
相交于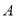 ,
, 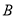 两点,当
两点,当 变化时,求
变化时,求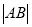 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,连接BM,MN,BN.
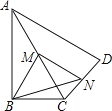
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆
 的左焦点为
的左焦点为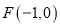 ,过点F做x轴的垂线交椭圆于A,B两点,且
,过点F做x轴的垂线交椭圆于A,B两点,且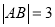 .
.(1)求椭圆C的标准方程:
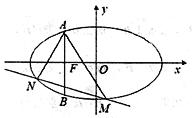
(2)若M,N为椭圆上异于点A的两点,且直线
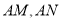 的倾斜角互补,问直线MN的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
的倾斜角互补,问直线MN的斜率是否为定值?若是,求出这个定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
北京市正围绕着“政治中心、文化中心、国际交往中心、科技创新中心”的定位,深入实施“人文北京、科技北京、绿色北京”的发展战略.“十二五”期间,北京市文化创意产业展现了良好的发展基础和巨大的发展潜力,已经成为首都经济增长的支柱产业.
2011年,北京市文化创意产业实现增加值1938.6亿元,占地区生产总值的12.2%.2012年,北京市文化创意产业继续呈现平稳发展态势,实现产业增加值2189.2亿元,占地区生产总值的12.3%,是第三产业中仅次于金融业、批发和零售业的第三大支柱产业.2013年,北京市文化产业实现增加值2406.7亿元,比上年增长9.1%,文化创意产业作为北京市支柱产业已经排到了第二位.2014年,北京市文化创意产业实现增加值2749.3亿元,占地区生产总值的13.1%,创历史新高,2015年,北京市文化创意产业发展总体平稳,实现产业增加值3072.3亿元,占地区生产总值的13.4%.
根据以上材料解答下列问题:
(1)用折线图将2011﹣2015年北京市文化创意产业实现增加值表示出来,并在图中标明相应数据;
(2)根据绘制的折线图中提供的信息,预估2016年北京市文化创意产业实现增加值约亿元,你的预估理由 .
相关试题

