【题目】已知函数![]()
(Ⅰ)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若对任意![]() 都有
都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设函数![]() ,求证:
,求证:![]()
.
参考答案:
【答案】(1)![]() 在
在![]() 上递增;(2)
上递增;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)由于![]() ,导函数的零点不能直接求出,考虑二次求导,求出
,导函数的零点不能直接求出,考虑二次求导,求出![]() 的最值,从而判断出函数
的最值,从而判断出函数![]() 的单调性;(2)由题意可知当
的单调性;(2)由题意可知当![]() 时,
时,![]() ,可通过讨论研究导函数的单调性和最值,得到
,可通过讨论研究导函数的单调性和最值,得到![]() 的最小值,得到参数
的最小值,得到参数![]() 的取值范围;(3)由题意可得
的取值范围;(3)由题意可得![]() ,可考虑证明两个和为
,可考虑证明两个和为![]() 的自变量对应的函数值的积为定值
的自变量对应的函数值的积为定值![]() ,通过整理
,通过整理![]() 并放缩可实现上述设想,最终得证.
并放缩可实现上述设想,最终得证.
试题解析:(1)![]() ,令
,令![]() ,则
,则![]() ,
,
则当![]() 时,
时,![]()
![]() 单调递减,当
单调递减,当![]() 时,
时,![]()
![]() 单调递增.
单调递增.
所以有![]() ,所以
,所以![]()
(2)当![]() 时,
时,![]() ,令
,令![]() ,则
,则![]() ,则
,则![]() 单调递增,
单调递增,![]()
当![]() 即
即![]() 时,
时,![]() ,
,![]() 成立;
成立;
当![]() 时,存在
时,存在![]() ,使
,使![]() ,则
,则![]() 减,则当
减,则当![]() 时,
时,![]() ,不合题意.综上
,不合题意.综上![]()
(3)![]() ,
,
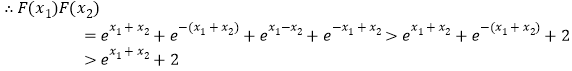
![]() ,
,
![]() ,……,
,……,![]() .
.
由此得,![]()
故![]() (
(![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若x,y∈[﹣1,1],x+y≠0有(x+y)[f(x)+f(y)]>0.
(1)判断f(x)的单调性,并加以证明;
(2)解不等式 ;
;
(3)若f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立.求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y2=2px过点P(1,1).过点(0,
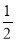 )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A为线段BM的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,所有棱长均为2,O是底面正方形ABCD中心,E为PC中点,则直线OE与直线PD所成角为( )

A.30°
B.60°
C.45°
D.90° -
科目: 来源: 题型:
查看答案和解析>>【题目】一直线l过直线l1:3x﹣y=3和直线l2:x﹣2y=2的交点P,且与直线l3:x﹣y+1=0垂直.
(1)求直线l的方程;
(2)若直线l与圆心在x正半轴上的半径为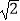 的圆C相切,求圆C的标准方程.
的圆C相切,求圆C的标准方程. -
科目: 来源: 题型:
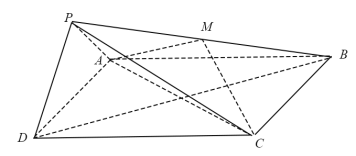
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD//平面MAC,PA=PD=
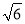 ,AB=4.
,AB=4.(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
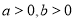 ,函数
,函数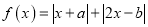 的最小值为1.
的最小值为1.(1)求
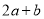 的值;
的值;(2)若
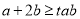 ,求实数
,求实数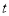 的最大值.
的最大值.
相关试题

