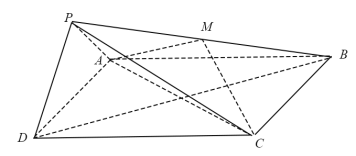
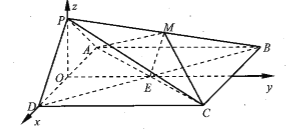
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.
参考答案:
【答案】(I)详见解析
(II)二面角![]() 为锐角的大小为
为锐角的大小为![]() .;
.;
(III)直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【解析】解:(I)设![]() 交点为
交点为![]() ,连接
,连接![]() .
.
因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 是正方形,所以
是正方形,所以![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中点.
的中点.
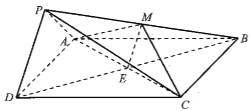
(II)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() .
.
又因为平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 是正方形,所以
是正方形,所以![]() .
.
如图建立空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则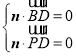 ,即
,即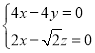 .
.
令![]() ,则
,则![]() ,
,![]() .于是
.于是![]() .
.
平面![]() 的法向量为
的法向量为![]() ,所以
,所以![]() .
.
由题知二面角![]() 为锐角,所以它的大小为
为锐角,所以它的大小为![]() .
.
(III)由题意知![]() ,
,![]() ,
,![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,所有棱长均为2,O是底面正方形ABCD中心,E为PC中点,则直线OE与直线PD所成角为( )

A.30°
B.60°
C.45°
D.90° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
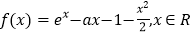
(Ⅰ)若
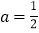 ,求函数
,求函数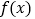 的单调区间;
的单调区间;(Ⅱ)若对任意
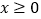 都有
都有 恒成立,求实数
恒成立,求实数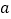 的取值范围;
的取值范围;(Ⅲ)设函数
 ,求证:
,求证: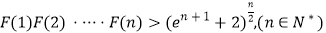
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一直线l过直线l1:3x﹣y=3和直线l2:x﹣2y=2的交点P,且与直线l3:x﹣y+1=0垂直.
(1)求直线l的方程;
(2)若直线l与圆心在x正半轴上的半径为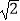 的圆C相切,求圆C的标准方程.
的圆C相切,求圆C的标准方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
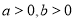 ,函数
,函数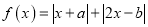 的最小值为1.
的最小值为1.(1)求
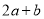 的值;
的值;(2)若
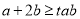 ,求实数
,求实数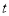 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,BC=2AB=4,
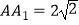 ,E是A1D1的中点.
,E是A1D1的中点.
(Ⅰ)在平面A1B1C1D1内,请作出过点E与CE垂直的直线l,并证明l⊥CE;
(Ⅱ)设(Ⅰ)中所作直线l与CE确定的平面为α,求点C1到平面α的距离.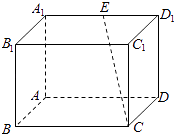
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2 , 若对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立,则实数t的取值范围是 .
相关试题

