【题目】一直线l过直线l1:3x﹣y=3和直线l2:x﹣2y=2的交点P,且与直线l3:x﹣y+1=0垂直.
(1)求直线l的方程;
(2)若直线l与圆心在x正半轴上的半径为 ![]() 的圆C相切,求圆C的标准方程.
的圆C相切,求圆C的标准方程.
参考答案:
【答案】
(1)解:直线l1:3x﹣y=3和直线l2:x﹣2y=2的交点P(0.8,﹣0.6),
设直线l的方程x+y+c=0,代入P,可得0.8﹣0.6+c=0,∴c=﹣0.2,
∴设直线l的方程x+y﹣0.2=0
(2)解:设圆心坐标为(a,0)(a>0),则 ![]() ,∴a=2.2,
,∴a=2.2,
∴圆C的标准方程(x﹣2.2)2+y2=2
【解析】(1)联立两个直线解析式先求出l1和l2的交点坐标,然后利用直线与直线l3垂直,根据斜率乘积为﹣1得到直线l的斜率,写出直线l方程即可;(2)利用圆心到直线的距离等于半径,求出圆心坐标,即可求圆C的标准方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y2=2px过点P(1,1).过点(0,
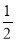 )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A为线段BM的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,所有棱长均为2,O是底面正方形ABCD中心,E为PC中点,则直线OE与直线PD所成角为( )

A.30°
B.60°
C.45°
D.90° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
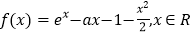
(Ⅰ)若
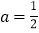 ,求函数
,求函数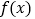 的单调区间;
的单调区间;(Ⅱ)若对任意
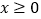 都有
都有 恒成立,求实数
恒成立,求实数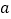 的取值范围;
的取值范围;(Ⅲ)设函数
 ,求证:
,求证: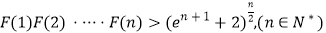
.
-
科目: 来源: 题型:
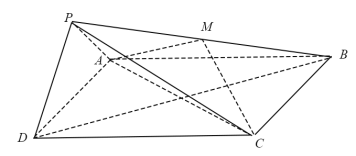
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD//平面MAC,PA=PD=
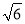 ,AB=4.
,AB=4.(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
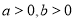 ,函数
,函数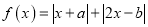 的最小值为1.
的最小值为1.(1)求
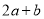 的值;
的值;(2)若
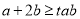 ,求实数
,求实数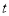 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,BC=2AB=4,
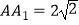 ,E是A1D1的中点.
,E是A1D1的中点.
(Ⅰ)在平面A1B1C1D1内,请作出过点E与CE垂直的直线l,并证明l⊥CE;
(Ⅱ)设(Ⅰ)中所作直线l与CE确定的平面为α,求点C1到平面α的距离.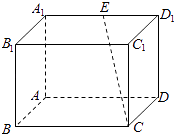
相关试题

