【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍。设购进A掀电脑x台,这100台电脑的销售总利润为y元。
①求y与x的关系式;
②该商店购进A型、B型各多少台,才能使销售利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台。若商店保持两种电脑的售价不变,请你以上信息及(2)中的条件,设计出使这100台电脑销售总利润最大的进货方案。
参考答案:
【答案】(1)每台A型电脑的销售利润为100元,每台B型电脑的销售利润为150元;(2)商店购进A型电脑34台,B型电脑66台,才能使销售总利润最大;(3)即商店购进70台A型电脑和30台B型电脑才能获得最大利润.
【解析】试题分析:(1)依据题设条件每台A型电脑的销售利润为a元,每台B型电脑的销售利润为b元建立方程组![]() 进行求解;(2)①根据题意建立目标函数y=100x+150(100-x);②根据题意建立不等式100-x≤2x进行分析求解;(3)据题意建立目标函数y=(100+m)x+150(100-x),然后运用分类整合思想对参数进行分类讨论求其最大值。
进行求解;(2)①根据题意建立目标函数y=100x+150(100-x);②根据题意建立不等式100-x≤2x进行分析求解;(3)据题意建立目标函数y=(100+m)x+150(100-x),然后运用分类整合思想对参数进行分类讨论求其最大值。
解:(1)设每台A型电脑的销售利润为a元,每台B型电脑的销售利润为b元,
则有![]() 解得
解得![]()
即每台A型电脑的销售利润为100元,每台B型电脑的销售利润为150元.
(2)①根据题意得y=100x+150(100-x),即y=-50x+15000
②根据题意得100-x≤2x,解得x≥33![]() ,
,
∵y=-50x+15000,-50<0,∴y随x的增大而减小.
∵x为正整数,∴当x=34最小时,y取最大值,此时100-x=66.
即商店购进A型电脑34台,B型电脑66台,才能使销售总利润最大
(3)根据题意得y=(100+m)x+150(100-x),即y=(m-50)x+15000.
33![]() ≤x≤70.
≤x≤70.
①当0<m<50时,m-50<0,y随x的增大而减小.
∴当x =34时,y取得最大值.
即商店购进34台A型电脑和66台B型电脑才能获得最大利润;
②当m=50时,m-50=0,y=15000.
即商店购进A型电脑数最满足33![]() ≤x≤70的整数时,均获得最大利润;
≤x≤70的整数时,均获得最大利润;
③当50<m<100时,m-50>0,y随x的增大而增大.
∴x=70时,y取得最大值.
即商店购进70台A型电脑和30台B型电脑才能获得最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一盒中放有的黑球和白球,其中黑球4个,白球5个.
(1)从盒中同时摸出两个球,求两球颜色恰好相同的概率.
(2)从盒中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
(3)从盒中不放回的每次摸一球,若取到白球则停止摸球,求取到第三次时停止摸球的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若
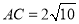 ,CE∶EB=1∶4,求CE的长.
,CE∶EB=1∶4,求CE的长.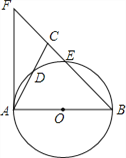
-
科目: 来源: 题型:
查看答案和解析>>【题目】某幼儿园为训练孩子的数字运算能力,在一个盒子里装有标号为1,2,3,4,5的卡片各2张,让孩子从盒子里任取3张卡片,按卡片上最大数字的9倍计分,每张卡片被取出的可能性都相等,用X表示取出的3张卡片上的最大数字
(1)求取出的3张卡片上的数字互不相同的概率;
(2)求随机变量x的分布列;
(3)若孩子取出的卡片的计分超过30分,就得到奖励,求孩子得到奖励的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
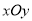 中,曲线
中,曲线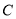 的参数方程为
的参数方程为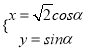 (
(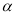 为参数),以原点
为参数),以原点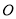 为极点,
为极点, 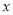 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线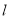 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
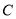 的普通方程与直线
的普通方程与直线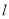 的直角坐标方程;
的直角坐标方程;(2)设
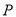 为曲线
为曲线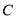 上的动点,求点
上的动点,求点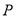 的直线
的直线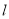 的距离的最小值.
的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.

(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀,请填写下面的
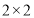 列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.甲班
乙班
合计
优秀
不优秀
合计
下面临界值表供参考:
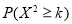
0.15
0.10
0.05
0.025
0.010
0.005
0.001
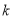
span>2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:
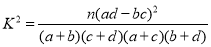 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题13分)已知函数f(x)=
 -
- (a>0,x>0).
(a>0,x>0).(1)求证:f(x)在(0,+∞)上是单调递增函数;
(2)若f(x)在[
 ,2]上的值域是[
,2]上的值域是[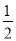 ,2],求a的值.
,2],求a的值.
相关试题

