【题目】已知函数![]() ,
,
(Ⅰ)若![]() ,求
,求![]() 的单调区间;(Ⅱ)若
的单调区间;(Ⅱ)若![]() 有最大值3,求
有最大值3,求![]() 的值;(Ⅲ)若
的值;(Ⅲ)若![]() 的值域是
的值域是![]() ,求
,求![]() 的取值范围。
的取值范围。
参考答案:
【答案】(Ⅰ)![]() 上单调递减,在
上单调递减,在![]() 单调递增. (Ⅱ)
单调递增. (Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
试题分析:(Ⅰ)将原函数分解为两个基本初等函数,借助于复合函数单调性判定方法可求得函数单调区间;(Ⅱ)由函数有最大值可知原函数先增后减,所以二次函数先减后增,及二次函数取得最小值-1,由此可得a的值;(Ⅲ)由函数值域可得![]() 可取的所有得正数,结合二次函数性质可求得
可取的所有得正数,结合二次函数性质可求得![]() 的取值范围
的取值范围
试题解析:(Ⅰ)当![]() 时,
时,![]() ,令
,令![]() ,由于
,由于![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减,而
单调递减,而![]() 在
在![]() 上单调递减,
上单调递减,![]()
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增. …………4分
单调递增. …………4分
(Ⅱ)令![]() ,
,![]() ,由于
,由于![]() 有最大值3,所以
有最大值3,所以![]() 应有最小值-1,因此
应有最小值-1,因此![]() ,解得
,解得![]() .…………8分
.…………8分
(Ⅲ)由指数函数的性质可知,要使![]() 的值域为
的值域为![]() ,则
,则![]() 的值域应为
的值域应为![]() ,因此只能是
,因此只能是![]() ,因为若
,因为若![]() ,则
,则![]() 为二次函数,值域不可能是
为二次函数,值域不可能是![]() ,故
,故![]() 的取值范围是
的取值范围是![]() .…12分
.…12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
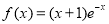 (
(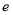 为自然对数的底数).
为自然对数的底数).(1)求函数
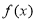 的单调区间;
的单调区间;(2)设函数
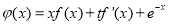 ,存在
,存在 ,
,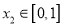 ,使得成立
,使得成立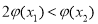 成立,求实数
成立,求实数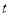 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
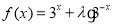 (
(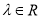 )
)(Ⅰ)当
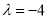 时,求解方程
时,求解方程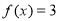 ;
;(Ⅱ)根据
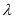 的不同取值,讨论函数的奇偶性,并说明理由.
的不同取值,讨论函数的奇偶性,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】侧棱垂直于底面的棱柱叫做直棱柱.
侧棱不垂直于底面的棱柱叫作斜棱柱.
底面是正多边形的直棱柱叫作正棱柱.
底面是平行四边形的四棱柱叫作平行六面体.
侧棱与底面垂直的平行六面体叫作直平行六面体.
底面是矩形的直平行六面体叫作长方体.
棱长都相等的长方体叫作正方体.
请根据上述定义,回答下面的问题(填“一定”、“不一定”“一定不”):
(1)直四棱柱________是长方体;
(2)正四棱柱________是正方体.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在区间
 上,若函数
上,若函数 为增函数,而函数
为增函数,而函数 为减函数,则称函数
为减函数,则称函数 为区间
为区间 上的“弱增”函数.则下列函数中,在区间
上的“弱增”函数.则下列函数中,在区间 上不是“弱增”函数的为( )
上不是“弱增”函数的为( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
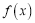 的定义域为D,如果
的定义域为D,如果 ,使得
,使得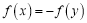 成立,则称函数
成立,则称函数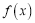 为“Ω函数”. 给出下列四个函数:①
为“Ω函数”. 给出下列四个函数:①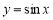 ;②
;②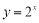 ;③
;③ ;④
;④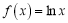 , 则其中“Ω函数”共有( )
, 则其中“Ω函数”共有( )A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据统计资料,我国能源生产自1992年以来发展很快,下面是我国能源生产总量(折合亿吨标准煤)的几个统计数据:1992年8.6亿吨,5年后的1997年10.4亿吨,10年后的2002年12.9亿吨.有关专家预测,到2007年我国能源生产总量将达到17.1亿吨,则专家是依据下列哪一类函数作为数学模型进行预测的( )
A.一次函数 B.二次函数 C.指数函数 D.对数函数
相关试题

