【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)设函数![]() ,存在
,存在![]() ,
,![]() ,使得成立
,使得成立![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)
上单调递减;(2)![]()
【解析】
试题分析:(1)要求单调区间,先求出导函数![]() ,然后解不等式
,然后解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间;(2)要解决本小题的问题,首先进行问题的理解与转化:“存在
得减区间;(2)要解决本小题的问题,首先进行问题的理解与转化:“存在![]() ,
,![]() ,使得成立
,使得成立![]() 成立”,等价于“
成立”,等价于“![]() 时,
时,![]() ”,这样下面主要问题是求
”,这样下面主要问题是求![]() 的最大值与最小值.求出函数式
的最大值与最小值.求出函数式![]() ,再求出导数
,再求出导数![]() ,
,![]() ,由此分类,分三类:
,由此分类,分三类:![]() ,
,![]() ,
,![]() ,分别求得
,分别求得![]() 的最大值和最小值,然后解不等式
的最大值和最小值,然后解不等式![]() 可得
可得![]() 的范围.
的范围.
试题解析:(1)∵函数的定义域为![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)假设存在![]() ,
,![]() ,使得
,使得![]() 成立,则
成立,则![]() .
.
∵![]() ,
,
∴![]() .
.
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,就
,就![]() ;
;
②![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() ;
;
③![]() 时,在
时,在![]() ,
,![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() ,即
,即![]() (*)
(*)
由(1)知,![]() 在
在![]() 上单调递减,故
上单调递减,故![]() ,
,
而![]() ,所以不等式(*)无解.
,所以不等式(*)无解.
综上所述,存在![]() ,使得命题成立.
,使得命题成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于棱柱的说法中,错误的是( )
A. 三棱柱的底面为三角形
B. 一个棱柱至少有五个面
C. 若棱柱的底面边长相等,则它的各个侧面全等
D. 五棱柱有5条侧棱、5个侧面,侧面为平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个命题与它的逆命题,否命题,逆否命题这四个命题中( )
A. 假命题与真命题的个数相同
B. 真命题的个数是奇数
C. 真命题的个数是偶数
D. 假命题的个数是奇数
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:
①垂直于同一平面的两条直线相互平行;
②平行于同一平面的两条直线相互平行;
③若一条直线平行于一个平面内的无数条直线,那么这条直线平行于这个平面;
④若一条直线垂直于一个平面内的任一条直线,那么这条直线垂直于这个平面.
其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
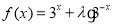 (
(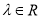 )
)(Ⅰ)当
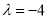 时,求解方程
时,求解方程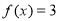 ;
;(Ⅱ)根据
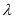 的不同取值,讨论函数的奇偶性,并说明理由.
的不同取值,讨论函数的奇偶性,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】侧棱垂直于底面的棱柱叫做直棱柱.
侧棱不垂直于底面的棱柱叫作斜棱柱.
底面是正多边形的直棱柱叫作正棱柱.
底面是平行四边形的四棱柱叫作平行六面体.
侧棱与底面垂直的平行六面体叫作直平行六面体.
底面是矩形的直平行六面体叫作长方体.
棱长都相等的长方体叫作正方体.
请根据上述定义,回答下面的问题(填“一定”、“不一定”“一定不”):
(1)直四棱柱________是长方体;
(2)正四棱柱________是正方体.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
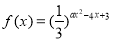 ,
,(Ⅰ)若
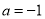 ,求
,求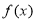 的单调区间;(Ⅱ)若
的单调区间;(Ⅱ)若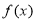 有最大值3,求
有最大值3,求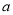 的值;(Ⅲ)若
的值;(Ⅲ)若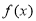 的值域是
的值域是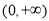 ,求
,求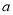 的取值范围。
的取值范围。
相关试题

