【题目】已知函数![]() (
(![]() )
)
(Ⅰ)当![]() 时,求解方程
时,求解方程![]() ;
;
(Ⅱ)根据![]() 的不同取值,讨论函数的奇偶性,并说明理由.
的不同取值,讨论函数的奇偶性,并说明理由.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() =1时,为偶函数;
=1时,为偶函数;![]() 时,函数为奇函数;
时,函数为奇函数;![]() 时,为非奇非偶函数
时,为非奇非偶函数
【解析】
试题分析:(1)当λ=-4时,令t=3x>0,则原方程可化为t2-3t-4=0,求得t的值,可得x的值.(2)函数的定义域为R,分当λ=1、当λ=-1、当|λ|≠1三种情况,分别根据奇偶函数的定义进行判断,可得结论.
试题解析:(Ⅰ)当![]() 时,由
时,由![]() ,得
,得![]() .
.
令![]() ,则原方程可化为
,则原方程可化为![]() ,解得
,解得![]() ,或
,或![]() (舍去),
(舍去),
所以,![]() .…………6分
.…………6分
(Ⅱ)函数的定义域为R,当![]() =1时,
=1时,![]() ,
,![]() ,函数为偶函数;
,函数为偶函数;
当![]() =﹣1时,
=﹣1时, ![]() ,
,![]() ,函数为奇函数;
,函数为奇函数;
当![]() 时,
时,![]() ,
,![]() ,
,
此时![]() 且
且![]() ,所以此时函数为非奇非偶函数.…………12分
,所以此时函数为非奇非偶函数.…………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个命题与它的逆命题,否命题,逆否命题这四个命题中( )
A. 假命题与真命题的个数相同
B. 真命题的个数是奇数
C. 真命题的个数是偶数
D. 假命题的个数是奇数
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:
①垂直于同一平面的两条直线相互平行;
②平行于同一平面的两条直线相互平行;
③若一条直线平行于一个平面内的无数条直线,那么这条直线平行于这个平面;
④若一条直线垂直于一个平面内的任一条直线,那么这条直线垂直于这个平面.
其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
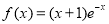 (
(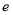 为自然对数的底数).
为自然对数的底数).(1)求函数
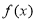 的单调区间;
的单调区间;(2)设函数
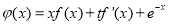 ,存在
,存在 ,
,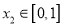 ,使得成立
,使得成立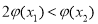 成立,求实数
成立,求实数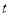 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】侧棱垂直于底面的棱柱叫做直棱柱.
侧棱不垂直于底面的棱柱叫作斜棱柱.
底面是正多边形的直棱柱叫作正棱柱.
底面是平行四边形的四棱柱叫作平行六面体.
侧棱与底面垂直的平行六面体叫作直平行六面体.
底面是矩形的直平行六面体叫作长方体.
棱长都相等的长方体叫作正方体.
请根据上述定义,回答下面的问题(填“一定”、“不一定”“一定不”):
(1)直四棱柱________是长方体;
(2)正四棱柱________是正方体.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
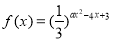 ,
,(Ⅰ)若
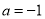 ,求
,求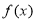 的单调区间;(Ⅱ)若
的单调区间;(Ⅱ)若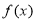 有最大值3,求
有最大值3,求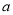 的值;(Ⅲ)若
的值;(Ⅲ)若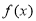 的值域是
的值域是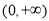 ,求
,求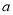 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在区间
 上,若函数
上,若函数 为增函数,而函数
为增函数,而函数 为减函数,则称函数
为减函数,则称函数 为区间
为区间 上的“弱增”函数.则下列函数中,在区间
上的“弱增”函数.则下列函数中,在区间 上不是“弱增”函数的为( )
上不是“弱增”函数的为( )A.
 B.
B. C.
C. D.
D.
相关试题

