【题目】如图所示,在四棱锥![]() 中,
中, ![]() 平面
平面![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 上的点且
上的点且![]() 为
为![]() 边
边![]() 上的高.
上的高.
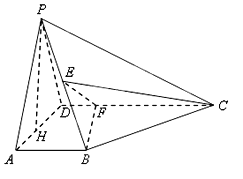
(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在这样一点
上是否存在这样一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,说出
?若存在,说出![]() 点的位置.
点的位置.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 中点.
中点.
【解析】试题分析:(1)![]() 平面
平面![]() ,
, ![]() 为
为![]() 中
中![]() 边上的高,
边上的高, ![]() ,由线面垂直的判定定理能够证明
,由线面垂直的判定定理能够证明![]() 平面
平面![]() ;(2)连接
;(2)连接![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() 是
是![]() 中点,
中点, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,由根据棱锥的体积公式能够求出三棱锥
,由根据棱锥的体积公式能够求出三棱锥![]() 的体积;(3)取
的体积;(3)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则因为
,则因为![]() 是
是![]() 的中点,先证明
的中点,先证明![]() ,再证明以
,再证明以![]() 平面
平面![]() ,可得
,可得![]() 面
面![]() ,即
,即![]() 与
与![]() 重合时符合题意.
重合时符合题意.
试题解析:(1)![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 又
又![]() ,
,![]() 平面
平面![]()
(2)![]() 是
是![]() 的中点,
的中点,![]() 到平面
到平面![]() 的距离
的距离![]() 等于点
等于点![]() 到平面
到平面![]() 距离的一半,即
距离的一半,即![]() =
=![]() ,又因为
,又因为![]() ,所以三棱锥
,所以三棱锥![]() ;
;
(3)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,则因为
,则因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,且
,且![]() ,又因为
,又因为![]() 且
且![]() ,所以
,所以![]() 且
且![]() ,所以四边形
,所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,由(1)知
,由(1)知![]() 平面
平面![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() 平面
平面![]() ,因为ED//DQ,所以
,因为ED//DQ,所以![]() 面
面![]() .M为PB中点.
.M为PB中点.
【方法点晴】本题主要考查线面垂直的判定定理及棱锥的体积公式,属于难题.解答空间几何体中垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;证明直线和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推论![]() ;(3)利用面面平行的性质
;(3)利用面面平行的性质![]() ;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 是圆心为
是圆心为 的圆
的圆 上的动点,点
上的动点,点 ,
,  为坐标原点,线段
为坐标原点,线段 的垂直平分线交
的垂直平分线交 于点
于点 .
.(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)过原点
 作直线
作直线 交(1)中的轨迹
交(1)中的轨迹 于点
于点 ,点
,点 在轨迹
在轨迹 上,且
上,且 ,点
,点 满足
满足 ,试求四边形
,试求四边形 的面积的取值范围.
的面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
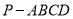 中,
中,  平面
平面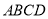 ,
, 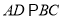 ,
, 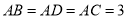 ,
, 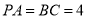 ,
, 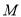 为线段
为线段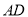 上一点,
上一点, 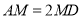 ,
, 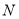 为
为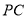 的中点.
的中点. 
(1)证明:
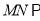 平面
平面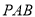 ;
;(2)求异面直线
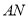 与
与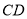 所成角的余弦值.
所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体
 的棱长为1,
的棱长为1, 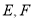 分别是棱
分别是棱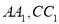 的中点,过直线
的中点,过直线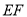 的平面分别与棱
的平面分别与棱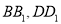 交于
交于 ,设
,设 ,
, 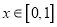 ,给出以下四个命题:
,给出以下四个命题:①
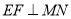
②当且仅当
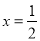 时,四边形
时,四边形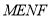 的面积最小;
的面积最小;③四边形
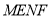 周长
周长 ,
,  ,则
,则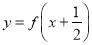 是奇函数;
是奇函数;④四棱锥
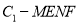 的体积
的体积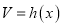 为常函数;
为常函数;其中正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点.
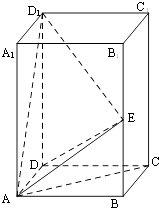
(1)证明:AC⊥D1E;
(2)求DE与平面AD1E所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x+2﹣x ,
(1)判断函数的奇偶性;
(2)用函数单调性定义证明:f(x)在(0,+∞)上为单调增函数;
(3)若f(x)=52﹣x+3,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn=3n+m(m为常数,n∈N+)
(1)求a1 , a2 , a3;
(2)若数列{an}为等比数列,求常数m的值及an;
(3)对于(2)中的an , 记f(n)=λa2n+1﹣4λan+1﹣7,若f(n)<0对任意的正整数n恒成立,求实数λ的取值范围.
相关试题

