【题目】已知点![]() 是圆心为
是圆心为![]() 的圆
的圆![]() 上的动点,点
上的动点,点![]() ,
, ![]() 为坐标原点,线段
为坐标原点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过原点![]() 作直线
作直线![]() 交(1)中的轨迹
交(1)中的轨迹![]() 于点
于点![]() ,点
,点![]() 在轨迹
在轨迹![]() 上,且
上,且![]() ,点
,点![]() 满足
满足![]() ,试求四边形
,试求四边形![]() 的面积的取值范围.
的面积的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】【试题分析】(1)借助椭圆的定义分析求解;(2)先借助题设将题设条件进行等价转化,再建立目标函数运用基本不等式进行分析探求:
(1)由于点![]() 在线段
在线段![]() 的垂直平分线上,故
的垂直平分线上,故![]() ,因此
,因此![]() ,故点
,故点![]() 轨迹为椭圆,其中
轨迹为椭圆,其中![]() ,
, ![]() ,因此
,因此![]() 点的轨迹
点的轨迹![]() 的方程为
的方程为![]() .
.
(2)由![]() ,知四边形
,知四边形![]() 为平行四边形,故
为平行四边形,故![]() .
.
(i)当![]() 为长轴(或短轴)时,依题意,知点
为长轴(或短轴)时,依题意,知点![]() 就是椭圆的上下顶点(或左右顶点),此时
就是椭圆的上下顶点(或左右顶点),此时![]() ,即
,即![]() .
.
(ii)当直线![]() 的斜率存在且不为0时,设斜率为
的斜率存在且不为0时,设斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,联立方程
,联立方程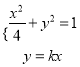 ,消去
,消去![]() ,得
,得![]() ,故
,故![]() ,
, ![]() ,
,
所以![]() ,由
,由![]() ,知
,知![]() 为等腰三角形,
为等腰三角形, ![]() 为
为![]() 的中点,所以
的中点,所以![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
同理,得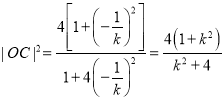 ,
,
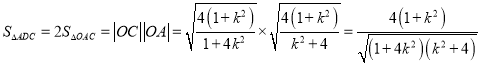 ,
,
设![]() ,则
,则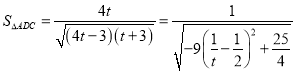 ,
,
而![]() ,所以当
,所以当![]() 时,
时, ![]() ,又
,又![]() ,所以
,所以![]() ,
,
所以![]() ,
,
综上所述, ![]() .
.
所以四边形![]() 的面积的取值范围为
的面积的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=sinxcosx将 f(x)的图象向右平移
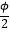 (0<φ<π) 个单位,得到y=g(x)图象且g(x)的一条对称轴是直线x=
(0<φ<π) 个单位,得到y=g(x)图象且g(x)的一条对称轴是直线x=  .
.
(1)求φ;
(2)求函数y=g(x)的单调增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正三棱锥
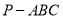 ,已知
,已知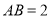 ,
, 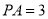
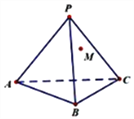
(1)求此三棱锥内切球的半径.
(2)若
 是侧面
是侧面 上一点,试在面
上一点,试在面 上过点
上过点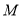 画一条与棱
画一条与棱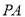 垂直的线段,并说明理由.
垂直的线段,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
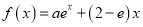 (
(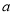 为实数,
为实数, 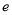 为自然对数的底数),曲线
为自然对数的底数),曲线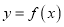 在
在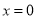 处的切线与直线
处的切线与直线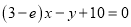 平行.
平行.(1)求实数
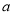 的值,并判断函数
的值,并判断函数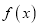 在区间
在区间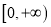 内的零点个数;
内的零点个数;(2)证明:当
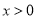 时,
时, 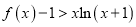 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,
中,  平面
平面 ,
,  ,
, 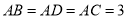 ,
, 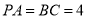 ,
, 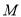 为线段
为线段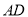 上一点,
上一点, 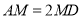 ,
,  为
为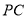 的中点.
的中点. 
(1)证明:
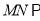 平面
平面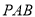 ;
;(2)求异面直线
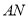 与
与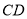 所成角的余弦值.
所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体
 的棱长为1,
的棱长为1, 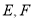 分别是棱
分别是棱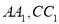 的中点,过直线
的中点,过直线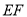 的平面分别与棱
的平面分别与棱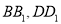 交于
交于 ,设
,设 ,
, 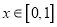 ,给出以下四个命题:
,给出以下四个命题:①
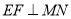
②当且仅当
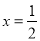 时,四边形
时,四边形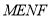 的面积最小;
的面积最小;③四边形
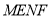 周长
周长 ,
,  ,则
,则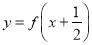 是奇函数;
是奇函数;④四棱锥
 的体积
的体积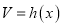 为常函数;
为常函数;其中正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥
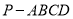 中,
中, 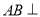 平面
平面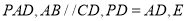 是
是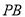 的中点,
的中点, 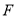 是
是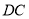 上的点且
上的点且 为
为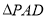 边
边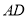 上的高.
上的高.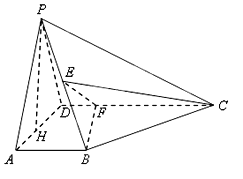
(1)证明:
 平面
平面 ;
;(2)若
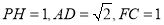 ,求三棱锥
,求三棱锥 的体积;
的体积;(3)在线段
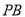 上是否存在这样一点
上是否存在这样一点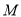 ,使得
,使得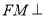 平面
平面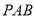 ?若存在,说出
?若存在,说出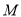 点的位置.
点的位置.
相关试题

