【题目】已知数列{an}的前n项和Sn=3n+m(m为常数,n∈N+)
(1)求a1 , a2 , a3;
(2)若数列{an}为等比数列,求常数m的值及an;
(3)对于(2)中的an , 记f(n)=λa2n+1﹣4λan+1﹣7,若f(n)<0对任意的正整数n恒成立,求实数λ的取值范围.
参考答案:
【答案】
(1)解:a1=S1=2+m,
由S2=a1+a2,得a2=2,
由S3=a1+a2+a3,得a3=4
(2)解:∵a1=a+2,当n≥2时, ![]() ,
,
又{an}为等比数列,∴a1=1,
即m+2=1,得m=﹣1,
故 ![]()
(3)解:∵ ![]() ,∴f(n)=λ22n﹣4λ2n﹣7,
,∴f(n)=λ22n﹣4λ2n﹣7,
令t=2n,则t≥2,f(n)=λt2﹣4λt﹣7=λ(t﹣2)2﹣4λ﹣7,
设g(t)=λ(t﹣2)2﹣4λ﹣7,
当λ=0时,f(n)=﹣7<0恒成立,
当λ>0时,g(t)=λ(t﹣2)2﹣4λ﹣7对应的点在开口向上的抛物线上,
∴f(n)<0不可能恒成立,
当λ<0时,g(t)=λ(t﹣2)2﹣4λ﹣7在t≥2时有最大值﹣4λ﹣7,
∴要使f(n)<0对任意的正整数n恒成立,
只需﹣4λ﹣7<0,即 ![]() ,此时
,此时 ![]() ,
,
综上实数λ的取值范围为 ![]() .
.
【解析】(1)由 ![]() ,能求出a1 , a2 , a3 . (2)由a1=a+2,当n≥2时,
,能求出a1 , a2 , a3 . (2)由a1=a+2,当n≥2时, ![]() ,{an}为等比数列,求出a1=1,由此能求出常数m的值及an . (3)由
,{an}为等比数列,求出a1=1,由此能求出常数m的值及an . (3)由 ![]() ,得f(n)=λ22n﹣4λ2n﹣7,令t=2n , 则t≥2,f(n)=λt2﹣4λt﹣7=λ(t﹣2)2﹣4λ﹣7,设g(t)=λ(t﹣2)2﹣4λ﹣7,由此能求出实数λ的取值范围.
,得f(n)=λ22n﹣4λ2n﹣7,令t=2n , 则t≥2,f(n)=λt2﹣4λt﹣7=λ(t﹣2)2﹣4λ﹣7,设g(t)=λ(t﹣2)2﹣4λ﹣7,由此能求出实数λ的取值范围.
【考点精析】解答此题的关键在于理解等比数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() ,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系
,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系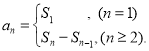 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥
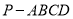 中,
中, 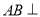 平面
平面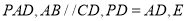 是
是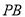 的中点,
的中点, 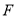 是
是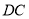 上的点且
上的点且 为
为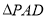 边
边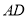 上的高.
上的高.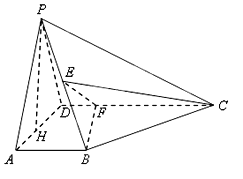
(1)证明:
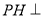 平面
平面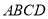 ;
;(2)若
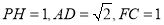 ,求三棱锥
,求三棱锥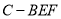 的体积;
的体积;(3)在线段
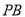 上是否存在这样一点
上是否存在这样一点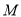 ,使得
,使得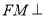 平面
平面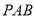 ?若存在,说出
?若存在,说出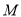 点的位置.
点的位置. -
科目: 来源: 题型:
查看答案和解析>>【题目】在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点.
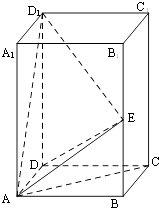
(1)证明:AC⊥D1E;
(2)求DE与平面AD1E所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x+2﹣x ,
(1)判断函数的奇偶性;
(2)用函数单调性定义证明:f(x)在(0,+∞)上为单调增函数;
(3)若f(x)=52﹣x+3,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
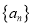 为公差不为
为公差不为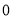 的等差数列,
的等差数列, 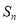 为前
为前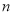 项和,
项和, 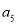 和
和 的等差中项为
的等差中项为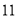 ,且
,且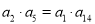 .令
.令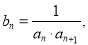 数列
数列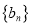 的前
的前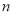 项和为
项和为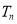 .
.(1)求
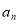 及
及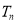 ;
;(2)是否存在正整数
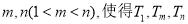 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的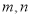 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
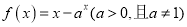 .
.(1)当
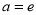 ,
, 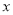 取一切非负实数时,若
取一切非负实数时,若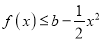 ,求
,求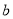 的范围;
的范围;(2)若函数
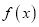 存在极大值
存在极大值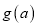 ,求
,求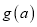 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市共有初中学生270000人,其中初一年级,初二年级,初三年级学生人数分别为99000,90000,81000,为了解该市学生参加“开放性科学实验活动”的意向,现采用分层抽样的方法从中抽取一个容量为3000的样本,那么应该抽取初三年级的人数为( )
A.800
B.900
C.1000
D.1100
相关试题

