【题目】在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点. 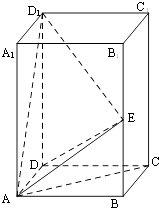
(1)证明:AC⊥D1E;
(2)求DE与平面AD1E所成角的正弦值.
参考答案:
【答案】
(1)证明:连接BD
∵ABCD﹣A1B1C1D1是长方体,
∴D1D⊥平面ABCD,
又AC平面ABCD
∴D1D⊥AC
在长方形ABCD中,AB=BC
∴BD⊥AC
又BD∩D1D=D
∴AC⊥平面BB1D1D,
而D1E平面BB1D1D
∴AC⊥D1E
(2)解:如图建立空间直角坐标系D﹣xyz,则A(1,0,0),D1(0,0,2),E(1,1,1),B(1,1,0), ![]()
设平面AD1E的法向量为 ![]() ,则
,则 ![]() ,
,
令z=1,则 ![]()
∴cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]()
∴DE与平面AD1E所成角的正弦值为 ![]()

【解析】(1)根据已知中长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点,结合长方体的几何特征,我们可得D1D⊥AC,BD⊥AC,结合线面垂直的判定定理即可得到AC⊥平面BB1D1D,即可得出结论;(2)建立空间直角坐标系,求出平面AD1E的法向量,利用向量的夹角公式,即可求DE与平面AD1E所成角的正弦值.
【考点精析】利用空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
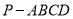 中,
中,  平面
平面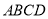 ,
, 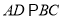 ,
, 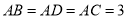 ,
, 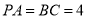 ,
, 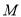 为线段
为线段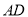 上一点,
上一点, 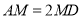 ,
, 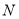 为
为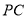 的中点.
的中点. 
(1)证明:
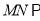 平面
平面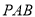 ;
;(2)求异面直线
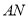 与
与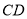 所成角的余弦值.
所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体
 的棱长为1,
的棱长为1, 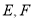 分别是棱
分别是棱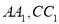 的中点,过直线
的中点,过直线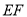 的平面分别与棱
的平面分别与棱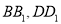 交于
交于 ,设
,设 ,
, 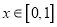 ,给出以下四个命题:
,给出以下四个命题:①
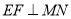
②当且仅当
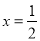 时,四边形
时,四边形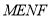 的面积最小;
的面积最小;③四边形
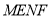 周长
周长 ,
,  ,则
,则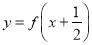 是奇函数;
是奇函数;④四棱锥
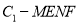 的体积
的体积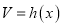 为常函数;
为常函数;其中正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥
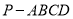 中,
中, 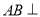 平面
平面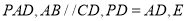 是
是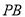 的中点,
的中点, 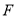 是
是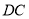 上的点且
上的点且 为
为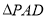 边
边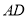 上的高.
上的高.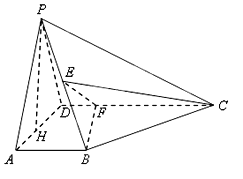
(1)证明:
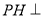 平面
平面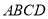 ;
;(2)若
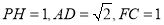 ,求三棱锥
,求三棱锥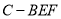 的体积;
的体积;(3)在线段
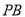 上是否存在这样一点
上是否存在这样一点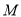 ,使得
,使得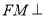 平面
平面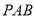 ?若存在,说出
?若存在,说出 点的位置.
点的位置. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x+2﹣x ,
(1)判断函数的奇偶性;
(2)用函数单调性定义证明:f(x)在(0,+∞)上为单调增函数;
(3)若f(x)=52﹣x+3,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn=3n+m(m为常数,n∈N+)
(1)求a1 , a2 , a3;
(2)若数列{an}为等比数列,求常数m的值及an;
(3)对于(2)中的an , 记f(n)=λa2n+1﹣4λan+1﹣7,若f(n)<0对任意的正整数n恒成立,求实数λ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
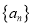 为公差不为
为公差不为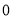 的等差数列,
的等差数列, 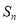 为前
为前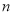 项和,
项和, 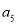 和
和 的等差中项为
的等差中项为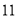 ,且
,且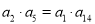 .令
.令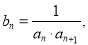 数列
数列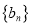 的前
的前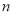 项和为
项和为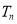 .
.(1)求
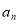 及
及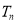 ;
;(2)是否存在正整数
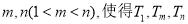 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的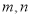 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

